interview
ビッグデータ時代の到来!
問題解決力育成に向けて変わる日本の統計教育
慶應義塾大学大学院健康マネジメント研究科教授 渡辺美智子先生

2007年の国会で新しい統計法が可決・成立し、戦後間もなく成立した旧統計法が60年ぶりに改正され2009年より全面施行されています。これによって、国が作成する公的統計情報の位置付けが、「行政のための統計」から「社会の情報基盤としての統計」に替りました。知識創造型社会が謳われる現在、社会や経済活動、科学研究から身近な生活に至るまで、日々創出される知識の裏付けとなる統計情報の有用性が高まり、公的統計・民間統計と範囲を限定することなく、事実上のビッグデータ時代が到来したのです。ビッグデータの扱いがビジネスの命運のカギを握ると言われています。
このような社会背景の中で、統計教育の重要性が日本でも認識され、新しい学習指導要領でも統計内容の拡充が図られています。国際社会が世界共通の力として目指す21世紀型スキル、その基盤となる問題解決力育成に向けた統計教育が現在の日本でも必要になってきています。問題解決型の統計教育とは何なのか、統計学がご専門の渡辺美智子先生にお話を伺いました。
予測不可能な未来に必要とされるのは、データに基づく問題解決の力
ニューヨークタイムズ紙の中で「2011年度にアメリカの小学校に入学した子どもたちの65%は、大学卒業時に今は存在していない職業に就くだろう」という予測が出て以来、今存在しない職業を意識した学校教育の在り方や子どもたちに付けてあげるべき力(21世紀型スキル)の議論が盛んになっています。世界中で何がどうなるのか将来の予測ができない時代において、既存の専門知識や技術の修得のみを目指すのではなく、課題発見と問題解決力、創造力、分析力、批判的思考力などの、未知の課題に立ち向かう思考方法や行動特性の育成に教育の軸足が移ってきています。
新課程での高校の教科「情報」においては、ICTを活用した問題解決力が強調されていますが、そこでは、客観的なデータに基づく問題解決の内容が取り扱われています。必履修化された新課程数学科の数学 I にも、「データの分析」の単元がありますが、教科「情報」においてはより大きな枠組みで、データに基づく問題解決の実践的な力の育成が求められています。データに基づいて問題解決をするためには、統計的なモノゴトの捉え方や処理の仕方が必要になってきます。つまり、統計思考力が重要で、これまで数学の教科書で扱ってきたような、公式の暗記と適用や計算など唯一の正解を出すためのものではありません。統計思考力を一言で言うと、
●身の周りの不確実性を伴う諸現象(確率1や0で決まらない現象)をデータの収集とそこに現れるデータのばらつきで捉え、全体のばらつきを分布として記述し、解釈する力
●分布に基づいた推測の方法の概念を理解し、諸種の文脈(コンテクスト)の下で実践的に応用する力
●課題の発見と問題の具体化、データの収集と記述、データに基づく推測(一般化)を行う、一連の問題解決のプロセスを理解し、知識の創出というアクションにつなげる力
であると言えます。
欧米では小学校から問題解決のフレームを学ぶ
世界中にデータに基づく問題解決(Data-based Problem Solving)という言葉は広まったきっかけは、1980年代後半、Japan as No.1 として高品質な日本製品とそれを次々と作り出す日本の製造業における品質管理(Quality Control)の方法論が注目されたことにあります。品質管理では、製品の品質を計量的な指標で定義し、Plan-Do-Check-Actの所謂PDCAサイクルを具体的な個別課題で回すことで、品質の向上を図っていきます。ここでは、つねに客観的事実に基づく問題解決として、勘や経験による水かけ論ではない、データに基づく組織・グループの意思決定が求められます。トヨタなどで有名になった「カイゼン」の方式です。この方式は、敗戦後僅か30年で経済大国となった「日本の奇跡」の主要因と言われ、1990年代以降の欧米諸国はこの「カイゼン」の手法を研究し、産業界だけでなく大学・学校教育にまで導入したのでした。
情報の新しい教科書には、問題解決の単元の最初に、「PDCAサイクル」が扱われています。欧米の産業界では、「PDCAサイクル」を統計的問題解決のサイクルとしてより具体的に再構築した「シックスシグマ」という方式を取り入れています。それは次のDMAICのプロセスから成ります。
【DMAICによる問題解決】
D(Define the problem):問題となっている現象をデータ(指標、特性値)で定義する。
M(Measure the process):その現象(指標、特性値)を要因(現象に至るまでのプロセス:過程)を含めて多次元で捉え、そのデータを計測する。とくに、特性要因図などの原因と結果の関連を考察するブレーンストーミングが重要になる。
A(Analysis the process):現象(結果)のデータと原因(プロセスを構成する諸要因)のデータの相関分析、因果分析を行い、原因を特定する。
I(Improve the process):原因に対して対処を行い、現象を改善する
C(Control the process):プロセスを管理し、特性値の変動を制御する
この統計的問題解決のプロセスを子ども向けにしたのが、PPDACサイクルです。下記はニュージーランドの小中学校で配布されている資料です。

このように欧米では、まず、問題解決のフレームワーク全体像を理解させ、どのステップでどんな概念図やデータ処理を行えばいいのか、その具体的な活用方法を文脈に沿って学ばせていきます。例えば、小学校低学年から毎学年、統計的探究・科学的探究として、「仮説を立て、データを集めて検証する」という作業を繰り返しています。難しいものではなく、「前日の夕方、西の空が晴れたら、次の日は晴れる」くらいのお天気レベルから始めることができます。子どもたちは、すべてがすべて仮説どおりにならないばらつきがあることを理解し、だいたいの傾向で判断することに、リスクが伴うことも意識できます。リスクを管理するための確率モデルの素地を具体的な学年進行に応じた具体的な文脈で感じとっていくのです。
日本発の統計的品質管理の手法や教育体系を、欧米ではモノづくりの品質管理にとどめず、経済・金融・経営・行政・教育等のあらゆる領域のマネジメントに広げ、その実践と教育を重視してきました。しかし、日本では製造業におけるモノづくり教育にだけにとどまり、学校教育においても、問題解決のプロセスの教育は行われてきませんでした。また、一時期、学習指導要領から統計内容も大幅に削減され、前の指導要領では実質的に中学・高校での統計教育は行われてきませんでした。今回の高校の新課程数学科と情報科の中で、国際社会が世界共通の力として目指す21世紀型スキルの基盤となる統計的問題解決力の育成が効果的に行われることを期待しています。
XとYで考える問題解決~評価指標Yと要因Xの抽出が大事

統計的な問題解決の枠組みについてもう少しお話ししましょう。
問題解決の最初の一歩は、課題をデータで解ける問題として考えるために、課題の重要度を計測する客観的な評価指標(アウトカム)=Yを何にするかを決めることです。
例えば、レストランやホテルで、サービスの質向上のためにお客様満足度調査が行われていますが、「また来店しますか?」という項目を評価指標として設定し、次の来店に繋がる要因を味や従業員の接客態度などの満足度と関連付けて調査しています。医薬品開発の領域では、昔、抗がん剤開発と評価の初期段階では、評価指標(Y)は、「少しでも長く生きられること」即ち、生存時間が計測され、それに向かった薬品開発が行われていましたが、現在は、「患者がいかに日常機能を維持して生きられるか(命の質=Quality of Life)」を評価指標に、薬剤の開発や医療施策が決められています。
Yを動かす要因Xを特定するためには、「特性要因図」(フィッシュボーン・チャート/石川ダイアグラム:図3 ) やロジックツリーのような手法が用いられます。Yに至る要因を、モレなく、ムダなく、ダブリなく(MECE)表現する概念図です。あらゆる要因を想定するためには、さまざまな知識や経験が必要となるため、一人よりはグループでのブレインストーミングが重要になります。5-Whyといわれる「なぜなぜ問答」といった手法も有効です。
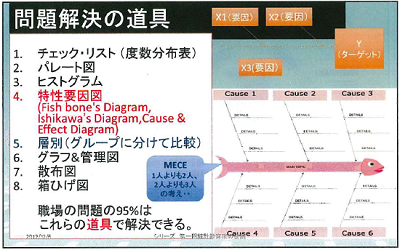
具体的なデータ処理の段階になると、度数分布表やヒストグラム、散布図などいろいろな計算やグラフ作成が出てきます。しかし、生徒には、統計的な道具を個別に学ばせるのではなく、それらが何のための道具で全体の問題解決全体のプロセスの中でどういう役割を果たすものなのか、つねにPPDACサイクルを意識させておくことが大切です。
データによる問題解決を教えるためにはどうしたらよいか
統計的なセンスや思考力は、実際に何度も具体的なデータの触れて問題解決を模擬体験することで養われるものです。先生方には、指導にあたっては、身近な問題と連動したいろいろなデータに触れさせて、データの集め方や処理に慣れさせてほしいと思います。
ともすれば、データの処理は、対象としている単一項目のデータにのみ着目して、そこから統計量を求めたりグラフを作成したりする指導で終わりがちですが、問題解決のストーリーの中でデータ処理の指導をするためには、物事を解釈をすることに慣れさせることも大事でしょう。結果だけを見るのではなく、その原因も考える癖をつけることが大切です。
「異性にもてる・もてない」を統計的に解決する
「不良品を減らす」や「売り上げを増やす」といった課題に対して統計を使った問題解決では、不良品の個数や売り上げ高の変動を観察して、その数値の上下の理由や原因を考える必要があります。つまり、その結果に至った「因果のルール」、「●●だから▲▲である」という、一般性のある法則を見つけるのがデータ分析の目的です。問題の背景が科学的な分野である必要はなく、解決の方法論が科学的(統計的)であればいいのです。
例えば、「異性にモテるようになりたい」ということについて考えてみましょう。これに科学的に対処するためには、必ず数値化できるものに落とし込むことが必要です。「モテる」をどう測るのか? 先ずこれを決めなければなりません。「異性から来るメールの数」なのか、「異性の友達の数」なのか。それを話し合いで決めたら(ここでは、「メールの数」を「モテる」ことの評価指標(アウトカム)にするとして説明します)、対象とする集団に対して、メールの数(これをY=目的変数とします)のデータを集めます。
このとき大事なのは、「20通のメールもらっている人もいれば、3通の人もいる」というデータのばらつきです。この20通と3通の差が生じる要因を科学的に分析するのが統計です。「所属する部活の違い」や「得意な科目の違い」などの要因(=X(説明変数))のうち、Yの変動を説明する要因が何かをデータで明らかにします。
個人の特性は授業ではなかなか扱い難いテーマかと思います。その場合は、スポーツなどの題材が生徒には身近で分かり易いのではないでしょうか。下図は、ワールドカップのデータから得点に繋がるプレーを探索するものです。

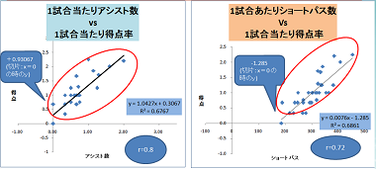
ビッグデータ化が進むと、データのサイズが量と質の面で大きく取れるようになってきます。単に、対象としている数がたくさんとれるだけではなく、一つひとつのデータの背景(説明変数X)がたくさん記録できるようになってきて、対象がヒトであれば、その属性や嗜好、行動履歴などが取れるし、スポーツの試合であれば、勝敗に至る経過のプレーがデータとして記録されるようになったということがポイントです。背景や経過の違いでデータを層別し結果がどう異なってくるのか、原因と結果のルールを見出していきます。
膨大なデータを処理するのはコンピュータです。統計ソフトも一般的になっていて、計算するのはパソコンの仕事。だとすれば、数学の教科書の統計の公式を覚えて、計算練習をたくさんするのは重要なことではありません。むしろ、問題解決の枠組みや分析のストーリーへの理解を深め、経験を積むことがより重要になってくるのでしょう。そのためには、コンピュータでデータを処理するスキルも必要になってきます。

情報の先生方には、先にお話しした、統計的問題解決のプロセスや、分析手法(図7参照)をしっかり教えていただきたいと思います。そのためにも、先生方には、統計的問題解決のサイクルを知る研修を、2日程度でけっこうですから、受けていただき、分析のおもしろさを味わっていただきたいと思います。
大学入試も、選抜方式から達成度評価をより重視する方式に変わるようなことも話題になっています。また、情報の入試を検討している大学もあります。日本統計学会では、「統計検定」の制度を設け、高校生が統計の活用力を評価する仕組みも作っています。
今後、ますますグローバル化が進めば、子どもたちが社会に出て仕事などで、海外の人と接することになります。彼らはみんなICTを活用した新しい時代の統計教育を受けてきています。毎年、アメリカでは12万人以上の高校生が、大学基礎レベルの統計検定試験AP Statisticsを受験しています。教科「情報」の先生方と共に、数学の先生方にも、問題解決型の統計教育、ビッグデータ時代のデータサイエンス教育の重要性を是非認識していただければと思います。
参考になる教材サイト
●グラフコンクール
なるほど統計学園(総務省統計局)「統計グラフコンクール」のページ
●教材の参考サイト
なるほど統計学園(総務省統計局)
小学生・中学生のための統計学習 「まなぼう統計」(東京都統計協会・東京都総務局統計部)
データで学ぶ統計活用のための教材サイト (統計関連学会連合)
今、求められる力を高める総合的な学習の時間の展開(小学校編)(文部科学省)
「第1編第2章 今、求められる力を高めるための学習指導」を参照
今、求められる力を高める総合的な学習の時間の展開(中学校編)(文部科学省)
「第1編第2章 今、求められる力を高めるための学習指導」を参照
渡辺美智子先生プロフィール
慶應義塾大学大学院健康マネジメント研究科教授。独立行政法人統計センター理事(研究主幹担当)、統計グラフ全国コンクール審査会委員長。
専門は統計学、とくに、多変量解析(潜在構造分析法)と統計教育。
九州大学理学部数学科から大学院総合理工学研究科情報システム学専攻に進んで、統計と情報学を学ぶ。大学院時代から、製薬企業主催の臨床統計の研究会にも参加。著書に『21世紀の統計科学III 数理・計算の統計科学』(分担執筆)東大出版会、『経営科学のニューフロンティア -マーケティングの数理モデル』(分担執筆)朝倉書店、『身近な統計(改訂新版)』(放送大学教育振興会)など。












