事例121

東京都立町田高校　小原格先生

1.　オーバーフローとアンダーフロー

一つ目が「オーバーフローとアンダーフロー(コンピュータが扱える数の範囲の限界)」です。

私はよく電卓を使いますが、スマホの電卓アプリでもいいでしょう。電卓の桁数は一般的に8～10桁程度ですが、今回は10桁の電卓を使い、桁数を目いっぱい使って計算します。

例えば、1,000,000,000に10をかける計算があります。計算自体は簡単ですが、答が10桁を超してしまいますからエラーになります。生徒たちもこれはわかります。

この場合のエラー表示は、桁があふれてしまっており、計算の正確性が保てていないということです。10桁の計算機は10桁まで、12桁の計算機は12桁までしか正確に計算できません。これは当たり前のことですが、「コンピュータの計算には限界がある」ということを説明できます。このあたりの話題は、半加算回路、全加算回路など、論理回路と2進法の計算や桁数の所と関連付けると効果的かと思います。

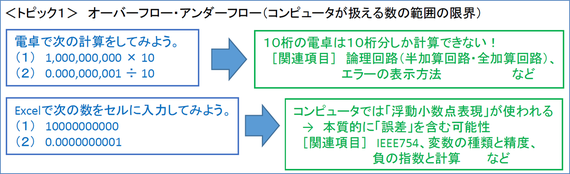
一方、0.0000000001÷10がどうなるかというと、0になってしまいます。この時エラーは表示されません。アンダーフローって、電卓の場合エラーが表示されないんですね。コンピュータは正確だといわれますが、生徒にこれを実演して見せたら、「コンピュータには限界があって、常に絶対的に正確な計算をするとは限らない」例にできるのではないでしょうか。

次にExcelです。先生方も使われていてご存知と思いますが、すごく大きな数、例えば100,000,000,000がセルに入ると、「########」と表示されたり、「1E+11」 などと表示されてしまいます。入力されている数値に見合う桁数がないとこのような表示になるようですが、だからといって、列の幅を増やしても，100,000,000,000　と表示されずに、1E+11　の表示のままだったりします。

セルの書式設定や入力した数の桁数などにも影響されるようですが、一般的に、非常に大きな数や非常に小さな数では、浮動小数点と呼ばれる表現が使われています。コンピュータは資源（メモリ等）に限界があるため、できるだけ効率よく利用し表現しようとしているわけです。そのため、桁数が非常に多かったり小数点以下の桁数の数値がたくさんあったりするような数の浮動小数点での表現では、限られた桁数で表されているため、入力された数が厳密に正確に表現されていないことが多く、そのため、結果には誤差が含まれている可能性が多分にあります。そういうところを授業で話題にするとよいと思います。

さらに、それに関連し、「倍精度・単精度とは何か」とか「浮動小数点の表現や計算のためにIEEE754という規格が決められている」というトピックを紹介してもよいでしょう。

そもそも、プログラミングをするときに、どの程度の数値を扱うのかということが精度にかかわってきます。Excelだったら、セルの書式設定が「標準」なのか「数値」なのかなど、そういうところに話題を持っていってもよいと思います。

それから、忘れてはいけないのが「負の累乗」です。例えば、10^-3などは、高校１年の初期の段階ではまだ学習していません。だから、－3乗ということを先取りして教える必要があります。このように、話題となる要素はけっこうたくさんあります。

2.　無理数などによる誤差、二進法による誤差（丸め誤差）

次は「無理数」のケースです。

例えば、√2×√2です。人間だったら「√2×√2＝2」とすぐわかります。ただし、無理数はコンピュータでは近似値になるので、切り捨てによる誤差が出るケースがあります。その時点ですでに正確な数ではありません。そのため、電卓で、√2×√2を計算させると、1.999999999　となり、数学的に正確な計算ができてはいません。

また、Excelを使って、4.3-4.2という計算をした場合です。セルの書式設定で表示形式の分類を「標準」にすると答は0.1になります。

ところがこの設定を「数値」にして、小数第20桁くらいまで表示させるようにすると、0.1にならず、0.09999999999999960000　と表示されます。これはどういうことかというと、二進法でいう0.1は、無限小数(循環小数)になります。だから、下が丸められて(切捨てられて)しまうのです。

このことから、例えばif関数で「4.3-4.2 は 0.1以上か」を判断させてみると、「真」ではなく「偽」になってしまい、「先生、何で? 」ということになります。ここで、二進法と丸め誤差を知っていれば「これは、実はね…」と、説明することができます。

ちなみにこれをプログラミングで計算させるとどうなるでしょうか。例えば、0.1を100万回くらい足すという設定をすると、最後の方は結果がずれてきます。ちりも積もれば……という感じですね。

何回足すのかというのを、プロンプトで入れさせるだけの単純なプログラムですが、プログラミングでもこれだけ誤差が生じるんだな、ということを実感させられます。

表計算ソフトの場合、0.1×○　のような単純な「かけ算」にすると、数値は正確に計算されますが、あえてセルに0.1をたくさん入力しsum関数の「足し算」にすると、誤差が大きくなる様子が見られます。ただし、100万個のセルに0.1を入力するのはコピーでも大変でしょうから、このような単純な繰り返し計算は、表計算ソフトよりもプログラミングが得意とするところかと思います。また、こういうふうにして誤差が出るので、誤差が生じにくいように、小数の場合は整数化し、計算後に少数に戻す等の工夫をすると良い、という指導もできるかと思います。

3.　計算上の注意(小数点演算の情報落ち、桁落ち誤差)

今までの話から、小数点の計算で、「すごく大きい数」「すごく小さい数」を演算するときは、注意が必要です。例えば、10桁の電卓で、1,000,000,000に0.4を3回足すという計算を行う場合を考えてみます。「1,000,000,000+0.4+0.4+0.4」とすると結果は1,000,000,000で変わりません。なぜかと言うと、0.4は、はじめの足し算の部分から桁落ちしてしまっており、「ない」と見なされているのです。

しかし、この計算を逆に「0.4+0.4+0.4＋1,000,000,000」とすると、1,000,000,001になります。さすがに0.2は桁落ちしてしまいますが、先ほどと比べ、若干精度が良くなっていることがわかります。

このように、コンピュータの計算の桁数というのは限界があるので、計算の精度を上げるには、計算の順番を工夫する必要があります。そういうことも含めて、計算には限界があるということが言えるかと思います。

また、「絶対値がほぼ等しい大きな数」どうしを引き算するときも注意が必要です。

数Ⅲを教えている先生は、平方根が含まれている極限の値を出すときに「分子の有理化」を指導されていると思います。つまり、分子が(無限大)-(無限大)にならないように、分子を有理化して分母に(無限大)＋(無限大)を作る。それと似たような考え方です。つまり、分子に平方根が含まれている場合、（すごく大きい平方根）－（すごく大きい平方根）では桁落ちで0になってしまう可能性があるのですが、分子を有利化し、分母を（すごく大きい平方根）＋（すごく大きい平方根）にしてしまえば、数値自体は非常に小さくなるけれども、ある程度の精度が期待できることになります。

なぜ、これを説明するのかというと、生徒に与えるプログラミングの題材を考えたとき、二次方程式で使う「解の公式」をプログラムし、実際にコンピュータに解を計算させる、というケースが多いのではないかと思われるからです。

二次方程式の解の公式の分子「－b±√(b^2-4ac)」の部分を計算させようとしたとき、もしもbが非常に大きく、かつ、4acが非常に小さかった場合、√(b^2-4ac)がbの値とかなり近くなります。その結果、－b＋√(b^2-4ac)の計算が桁落ちしてしまい、0となってしまう可能性が出てくるからです。そのため、そのような場合には分子の有利化をすることにより、分子の4acが残って、ある程度の精度が期待できることになります。

このように、コンピュータは極端な数の二次方程式を正確に計算できない場合があります。このような分子の有利化などの知識は、1年生ではまだ難しいかもしれませんが、3年生で情報Ⅱをやっている生徒なら、是非理解し活用して欲しい内容だと思っています。

これらの内容を先生方が理解をしておけば、「計算の限界」というトピックが出てきたときに、「何これ、わからない」とはならず、自信を持って教えることができると思います。

神奈川県高等学校教科研究会情報部会実践事例報告会2018　ポスターセッションより