今日の発表内容では、まず小中学校での統計・データの学習の扱いについてお話しします。その後、先行で実践されている方の事例や私自身の授業についてお話しし、最後にまとめということで進めたいと思います。

新学習指導要領の解説も出ていますし、来年から使われる小学校の教科書も既に展示が行われていますが、かなりすごいことになっているなというのが実感です。プログラミング必修化が世間の注目を集めていますが、確かに小学校から全員必修で始まるので、かなり大きなことだとは思います。それだけではなく、実は統計やデータの扱いも相当大きく変わってくるので、きちんと準備しておかないと非常に危ないのではないかという不安を感じているところです。

まず、小学校での変化を見ていきます。小学校の算数では、今までは「数量関係」といわれていたのが、「データの活用」ということで、『データ』という言葉が学習指導要領の中で出てきています。

具体的に何をやるかということを整理しました。ざっくり言って、1年生は個数を数えましょう。2年生は簡単な表を作りましょう。3年生は日時や場所に分類して棒グラフを作りましょう。4年生はデータを二つの観点で整理したり、2次元の表を作ったりしてクロス集計みたいな感じの集計をしましょう。そして折れ線グラフを書きましょう。5年生では「統計的な問題解決の考え方」というのが新しく入ってきます。また、円グラフ、帯グラフ、測定値の平均というのもここで学びます。6年生では代表値が中学校から移ってきています。ドットプロットという新しい言葉も出ています。さらに階級値、統計的な問題解決の方法ということで、PPDACというものも出てきます。6月の教科書展示のときに、算数の1年生から6年生までの教科書を全ページざっと目を通しましたが、驚いたのは何社かの教科書会社さんが、このPPDACという言葉を小学校の教科書にそのまま載せていました。

小学校でも出てくるということで、PPDACという流れを確認しておきます。Problemで問題の把握・設定。Planでデータの想定、収集計画。次にDataでデータの収集、表への整理。Analysisで分析としてグラフの作成や、特徴や傾向の把握。最後にConclusionで結論付け、振り返りです。PPDACはよくサイクルで書かれますが、それだけでなく、行き来しながら進みますよ、と小学校学習指導要領の解説にも書かれています。

中学校がこちらです。「資料の活用」といわれていたのが、「データの活用」と名前が変わりました。高校にあった累積度数が、中学校1年に降りています。あとヒストグラムですね。確率分野のほうでは、頻度確率が扱われています。2年生では、現行の高校1年の数学で行っている、データの分布の四分位範囲と箱ひげ図が中学校に下りてきて、ちょっと話題になったのでご存じの先生も多いかと思います。

確率の方では、場合の数によって得られる理論的な確率も2年生で学びます。3年生では標本調査をやります。中学校でこういったことを学んだ生徒たちが、高校に入ってきます。

高校の数学とのつながりも見ておきましょう。全員必履修の数学Iでは、分散、標準偏差、散布図、相関係数、外れ値、仮説検定の考え方が入ってきていますので、このあたりは、情報の学習指導要領解説でも「数学と連携しましょう」ということが書かれています。

数学Aでは、確率の中に期待値が復活します。数学Bは3分野があるので、どのような扱いになるかわかりませんが、統計が三つのうちの一つに入っていて、区間推定や仮説検定が内容に入っています。こんなところですが、やらなければならないことが大体見えてくるかと思います。

情報Iのデータの活用ではどのようなことが書かれているかを見ていきましょう。

ファイルの形式だけでなく、名義・順序・間隔・比例の四つの尺度の話、質的データ・量的データの話、欠損値・外れ値、テキストマイニング、仮説検定とあります。数学と関係するところに色を付けてみましたが、相当数学との連携を考えながらやっていかなければならないことがわかります。うまく数学とタイアップできるかどうか、というのが今後の課題だと思います。

ここからは先行事例のお話です。前々回の全高情研の全国大会で、横浜翠嵐高校の三井先生の発表を見て、すごく面白そうだなと思いました(※)。三井先生の発表は、グループワークで統計を活用した授業で、数的な検討が必要な2つの項目で相関分析をした一連の過程を発表させるということで、「納豆と握力の関係」とか「牛乳と骨折の関係」とか、とても面白い発表だなと思いました。

※「実際の授業から見える情報科における統計分野の実践と課題」

神奈川県立横浜翠嵐高校　三井栄慶先生　

[第10回全国高等学校情報教育研究会全国大会（東京大会）講演より]

当時は、主体的・対話的で深い学びになる学習活動として面白いなと思っていましたが、さらに三井先生の授業ですごいと思ったのは、求まった値を、生徒が評価して生徒自身で疑似相関ということに気が付いていくところで、なるほどそこまでできるんだと思いました。

今、実際に授業の計画を立てるときに、先ほどお話ししたような学習指導要領などと結び付けて考えると、三井先生の授業は自然にPPDACになっていたのだな、ということに気づきました。全国大会の発表というのは、自分の発表で終わるのでなく、他の人がやられたことを自分でやってみて、さらに広がっていくのはとてもすばらしいと思います。私が三井先生の発表を元にやってみたところで、PPDACとどのようにつながっていったかは、また後ほどお話しします。

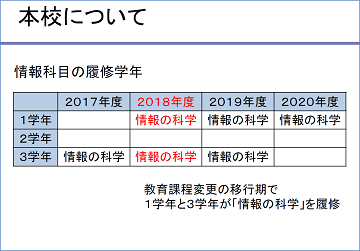
本校の状況を簡単にお話しします。現在の3年生までが「情報の科学」を3年生で履修するという教育課程になっていましたが、数年前に「もしかしたら情報Ⅰが入試に出るかも」という話が出たときに、「これは情報を1年生でやらないとまずいぞ」という話をして、1年生に入れてもらいました。そのような経緯から、昨年と今年はその過渡期になっており、1年生と3年生の二つの学年、18クラスで実施しているところです。情報の教員は私ともう一人おりまして、1年生は私中心で、3年生はもう一人の方が中心で昨年度の授業を行いました。

時期的に3年生が先にやりました。一斉授業の題材として、箱根駅伝の往路タイムと復路タイムの共分散・相関係数を求め、散布図を書き、さらに往路と復路のタイムに相関があると言えるのか、言えないのかということを行いました。

無相関検定ということで、欲張って両側・片側というところまでやってみました。授業では、説明の部分は一斉授業で行いました。

具体的な内容はこんなところです。

一斉授業のデータとしてはある年の箱根駅伝の往路と復路のタイムのデータを元に、帰無仮説と対立仮説を立てて、有意水準はよく統計で使われているようなパーセントにしましょうということで使いました。

計算式も示しました。ただ、なぜこうなるというところについては、以前に鹿野先生が「ある部分はブラックボックスにしておいても仕方ない」というお話をされていたので、ここは「この式で出ますよ」という扱いにして、自分たちで実際に値を出してみて、検定でどちらの仮説を採択するかということを行いました。

結論の言い方は、間違える可能性(過誤)もあるということで、一種の過誤、二種の過誤のところは、踏み込むことは避けましたが、表現としては断定しないで、間違いがあるかもしれませんよというところは意識しておきなさいよ、ということを一斉授業で伝えました。

このあと、グループでデータとして何か関係がありそうなものを見つけて、無相関検定を行って考察するという課題を出しました。

生徒が実際に考えたのは、「握力と腕の太さの関係」とか「1週間に飲む牛乳の量と身長の関係」「掌の大きさとスマホの入力の速さの関係」などといったものです。

この「掌の大きさ×スマホ入力」(Plan)を調べたグループでは、実際に掌の長さを測って、スマートフォンで「崖の上のポニョが横断歩道で側転」という言葉を入れる時間を何人も測って、それのデータを取りました(Data)。データでそれを検定して(Analysis)、分析・結論(Conclusion)と出していきました。実は、掌の大きさと入力速度には相関があるとは言えなかったのですが、もしかしたらスマホを使う時間と比べればよかったのではないかと言っていました。

次に1年生の方は、さすがに無相関検定はブラックボックスの部分が多過ぎますが、χ2検定をやりたかったので、1月頃にこの辺りの内容に合わせてやりました。

私が担当したところで一つ特徴なのが、マリメッコチャート(モザイク図)を書いて、χ2検定をしました。このスライドのように、実測度数と期待度数きれいに切れている場合とそうでない場合の比較ということで、図式化するというのがポイントです。

期待度数の計算でどうやって出すの、ということですが、右側の縦の辺の比率が、全体600分の306(「思う」人数)と294(「思わない」人数)です。このルールに注目して、生徒が自分で計算できるようにしています。χ2検定って何をやっているの、ということで、ここの差がある・ないということについて図を見ることで意識できるようにしました。

その後は、いわゆる仮説検定の流れです。自分で言葉を作っていくのはなかなか大変なので、テンプレート化して流れに乗っていけば検定の流れは追えると思います。

一斉授業のあと、グループ活動で生徒が興味を持った二つの項目の関係について調査をして、χ2検定を行ってくださいという課題を行いました。

生徒が見つけてきたテーマは、「スポーツを見ることの好き嫌いとプレーの得意・不得意」とか「たい焼きの中身の好みと、頭から食べる・尻尾から食べる」などです。

例えば、「たい焼を頭から食べるかどうか×あんの好み」については、結果的に相関はありませんでした。生徒はアンケートを作って、無作為抽出でアンケートを実施して、結果を集めて、図作って、クロス集計をかけて、検定をやって、結果を発表するスライドを作って…という一連の作業を行いました。このように、図式として捉えたことで、数値の意味を可視化するというところで、シミュレーションベースのほうがおそらく腑に落ちるだろうと思います。

授業の工夫としては、PPDACの流れがわかるようにしたこと、表計算ソフトに慣れさせたこと。あとは、仮説検定はテンプレート化して、二者択一で選んで埋めていくことにしたことです。今大会の他の先生の発表で、仮説検定の危うさというところもうかがったので、今後はその点もさらに考えていかなければならないと思いましたが、χ2検定の一通りの流れは一応追えるようにしたということです。

授業の成果としては、生徒は統計や調査・分析はほとんど経験がなかったので、とてもよい経験になったと言っています。グループ活動で普段話さない人と話すことができた、予想と結果の違いは分析して初めてわかることに気付いた、統計値から何が言えるのか、何を示すのか考えるのが難しかったけれど、グループで協力したり、他の班の発表を聞いたりして、数値や分析結果が理解できたという発言も得ています。

また、自分たちで検定を行ってうまくいかなかった場合も、それを見せるというのが大事だと思います。データを取るときに、表の作り方で結構いろいろな問題がありましたが、そういったことをデータベースとつなげていくところも必要かと思いました。

また尺度の話では、例えば「〇〇した年齢」を聞こうとして「したことがない」という欠損値が多数ありました。

どこまでブラックボックスにするか、というのも非常にすごく悩ましいところです。χ2検定でも、やはり説明しきれない部分は残っています。片側検定、両側検定、有意水準の決め方の話はとても難しいので、固定してしまってもよいかと思います。

χ2検定では期待度数が0になってしまって、検定不能というケースもありました。これは、人数がクラス単位だとちょっと少ないことにも関係します。イェイツの補正といった方法もありますが、不十分なデータということはどうしても残ります。

また、先ほど掌の大きさを測っていましたが、ああいったサイズを取るときに、プライバシーとか個人情報がどうなっているのかについて考える必要があるということも、指導しなければいけないと思います。