事例136
高校生が楽しく学べる仮説検定と相関・因果
シミュレーションから始まる「情報科」統計教育
日出学園中学校・高等学校 武善紀之先生
「情報」は「数学」の補助科目ではない

新学習指導要領では、データサイエンスが大きな目玉となっています。数学Ⅰに加え、情報Iでも仮説検定や相関・因果について扱うことが明示されています。

ただ、統計には苦手意識を持つ生徒が多く、どうしても、負のイメージがつきまといがちです。さらには今回の改訂で、情報=パソコン教室という誤ったイメージが補強され、「理屈で理解した内容のパソコン作業を行うのが『情報』」という思い込みにつながりそうで心配しています。

コンピュータは、あくまで情報を学ぶための手段の1つであり、決して情報=パソコン教室の時間ではないということを、生徒たちにはわかってほしいです。
とはいえ手段に陥ってはいけないと、統計の理屈を詳細に扱ってしまうと、時間的な制約もあり、結果として情報の授業が楽しくなくなってしまうという課題もあります。

情報科では、数学と同じ「統計学」的なアプローチを取る必要はありません。情報科には情報科らしい「統計法」的なアプローチがあるはずと思い、今回の実践に行き着きました。
数式を使わず、仮説検定を理解させるSBIモデルとは
これら背景を踏まえ、授業はプレゼン実習の改変として行いました。プレゼンのテーマをクラスの実態調査として、そこに仮説検定を利用します。こういったアンケート調査は、いろいろとオプションがつけられるので、ここに無理なく仮説検定を入れることができるからです。

さて、仮説検定について少し補足します。特進クラスのテストの平均点が72点、進学クラスが70点だったとします。私たちは、この点数だけを見て「特進クラスの方が優秀である」という結論を導きがちです。しかし、「果たして偶然性を排除できているのか」という疑問がここには生じます。

この疑問を解消するためには偶然と必然のバトルが必要で、それが仮説検定です。最初に「帰無仮説」で「差がない」ことを設定し、いろいろ計算をして、「偶然にしてはおかしなことが起きているぞ」、それなら「これはやっぱり偶然じゃないから、二つの間には差があるぞ」と導いていくのが、仮説検定の仕組みです。
ただし、ここに一般的なt検定を持ってくると、いろいろな数式が絡んできて、生徒たちは面倒くさくなり、やるのが嫌になってしまいます。
この最大の障壁、「理屈をどのように説明するか」という問題で、いろいろ探していたときに出会ったのがSBI(simulation-based inference)というモデルでした。Jimmy.A.Doi先生が、江戸川大学の情報教育研究会で発表されていたものです。SBIは「シミュレーションに基づく推論」ということで、いわゆる確率変数や密度関数などの数式を使わずに、統計を教える方法です。

以下、「」内は、Jimmy先生の説明です。
「仮説検定というのは、結局たったの3ステップです。つまり、仮説を立てて、実験をして証拠を集め、証拠に基づいた結論を出すということです。
例えば、コイントスをするときに、『まず、インチキかどうかを確認しよう』と言って、50回コインを投げるという実験をします。最初に25回表が出るという予測を立てますが、実際に試してみると24回ということもあるでしょう。これは、偶然だろうということで、もう一度試すと、22回になったりします。これもやはり偶然と言えるのではないだろうか。でも、さすがに2回になったら、これは明らかにインチキなコインだという判定ができます。これが、仮説検定のステップです」。

この説明をした後に、Jimmy先生は、赤ちゃんに対する心理実験の話を持ってきました。
「赤い玉が、坂を頑張って登ろうとしますが、上からは三角形が邪魔をしてくる、しかし、下からは四角形が助けてくれるという動画を、赤ちゃんに見せます。そして、この後、赤ちゃんに好きな画像を選択させると、16回中14回四角い方を選ぶのです。つまり、赤ちゃんは『手助けする行為』を理解できている、という研究です。
しかし、いきなりこの話をすると、生徒たちは『こんなことでわかるわけない』『たまたまでしょ』という言い方をするんです。

では、本当にたまたまということが起こり得るのかという疑問を検証するために、10円玉で16回コイントスをするという実験を行います。
コイントスをして、生徒にそれぞれ正の字を書かせ、表と裏を調べた後に、これをグラフにしてみます。「5回の人」「6回の人」と、順に手を上げさせてみると、結構きれいな山型になります。そして、14回ということは、ほぼありえない数だということがわかるわけです。非常に激レアなことが起きたということで、これは単なる偶然ではなく『赤ちゃんにも好みがある』という結論が導き出せるのです」。

このアプローチですが、実は数学Iの新学習指導要領解説にほとんど同じことが載っています。ただ、数学の教科書は数学らしく、そこから反復試行の計算に持っていってしまいます。しかし、Jimmy先生は、この後にコンピュータを用いた大規模シミュレーションへとさらに話を持っていきました。このようにデータを分析すれば、偶然と必然の切り分けができるということを、計算なしで生徒たちに理解させることに、成功しているのです。
アンケートでデータを集め、その分布からレア度を計る
この説明をした上で、生徒たちには実習に取り組んでもらいました。ただ、今の赤ちゃんの話は、いわゆる「二項検定」といわれるもので、「ある・ない」とか、「勝ち・負け」の判定になっているだけで、あまり展開が広がらないという面があります。一方で前述したt検定までいくと、それはそれで難易度が高く、少し踏み込み過ぎの感が否めません。「なんとなくわかる感」という程度がちょうどいいと思うのです。
では、生徒がわかるレベルでできる仮説検定とは何かということで、目を付けたのが、「フィッシャーの直接確率計算」という方法です。
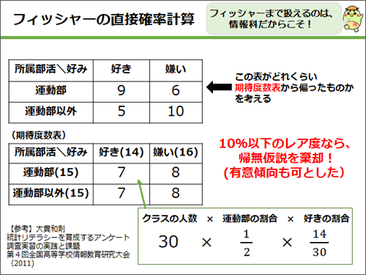
この手法については2011年に大貫和則先生もポスター製作実習の一環として発表されています。フィッシャーの直接確率計算とはクロス集計表を作って、この表のレア度を判定するというようなものです。
例えば、左上のマスについて。運動部が15人で運動好きが14人の場合、このマスに入る人数の期待値は7人になります。このぐらいの計算だったら、生徒たちも簡単にできます。この表から、極端にずれていたら偶然ではない理由になる、という説明の仕方をすると、生徒は仮説検定をそれなりにわかってくれたように感じました。
そこで、「実際に仮説検定を使って、クラスの実態調査をしよう」という課題を出しました。フィッシャーの直接確率計算を使うのなら、それほど大きく今までのプレゼンやアンケート実習の構成を変える必要はありません。唯一今までのアンケート調査から変えたのは、2×2のクロス集計表に落としこめる内容で作ろう、ということだけです。こうして縛りをつけることで、かえってテーマが考えやすくなったという生徒もいたので、内容としてはよかったのではないかと感じています。

特に、クロス集計で分析をすると、必ず四つのパターンに分岐ができるので、この4択だけを回収すればいいということになります。Googleフォームでアンケートを採れば、5分から10分くらいで集計まで終わります。
フィッシャーの検定は、Rの標準パッケージに入っているので、検定は全部コンピュータがやってくれて、p値まで出すことができます。

実習内容は単純ですが、生徒は事前に、仮説検定のメカニズムについて勉強しているので、突然難しい内容になったというような反応はしません。この結果に基づいて、プレゼンテーションを作り、総合評価をするというような授業を構築しました。これが実際のプリントです。正の字を書いて、確かめているのがわかると思います。

この実習の難しいところは、質的調査になるため、「運動が好き」とか「成績が良い」という質的データをいかに正確に取るか、というところです。主観を頑張って客観的な数字に落とし込むという作業を、ここで経験することができるのです。
結果的には全員に有意差が出るわけではありません。あるクラスでは28人中11人と、有意差が出た生徒は半分を切りましたが、むしろ有意にならない方が考察できる点もたくさんあり、発表はとてもしやすくなったようです。

こちらはプレゼンの例です。生徒たちは「兄弟がいると、先に食べられてしまわないように、好きなものを早く食べる癖がつくこと」を調べてみたとか、「雨が降るときに、小雨でも傘を差すのは、荷物が重かったり化粧をしていたりするから、男子より女子の方が多い気がする」というような、身近な問題を上手に見つけて調べていきます。ちなみに、この2つは、両方ともうまくいかず、有意差が出なかった例です。
しかし、単なる「好きなものプレゼン」と違って、コピー&ペーストに陥ることもなく、かつ、自分の立てた仮説のため、必死に考察しようとするので、見ていてもおもしろく、生徒たちが生き生きと楽しそうにやっているのがよかったです。

疑似相関に陥らないため「相関」と「因果」の学習は仮説検定と1セットに
ただし、実際に相関があったとしても、因果を示すわけではありません。
例えば、「運動部に入ると運動が好きになる」という仮説の下で、相関(今回の場合は連関)が出たとしても、もしかすると「運動が好きだから、運動部に入ったのでは」とか、「親がスポーツ熱心だから、運動部に入部させて、子どもも運動を好きになったのでは」ということなのかもしれません。いわゆる疑似相関です。疑似科学にだまされてしまうような状態で、生徒たちを放り出すわけにはいきません。検定を扱うのであれば、相関・因果を必ずセットでやらなければならないと、考え深めてみました。

さらに、相関・因果というのは、入試でも非常に出やすい単元です。SFC(慶應義塾大学湘南藤沢キャンパス)や明治大学のなどの実際の情報入試でもよく出ています。
慶應の商学部の論文テストは以前からかなり情報寄りで、今年も暗号化の問題など、ばっちり出ていました。慶應義塾大学の小論文の問題を元にして、授業のワークを作れば入試対応にもなるということで、相関・因果の二つを合わせ持つ問題を出してみました。

一つは慶應の商学部の論文テストで、相関と因果の違いの定義を答える問題です。因果には三つの法則があり、相関することはもちろん、時間的な順序関係が存在していて、かつ、他の原因を完全に排除できることが必要です。いろいろな疑似相関を書かせる問題があります。

もう一つ問題例を紹介します。2017年の、慶応の総合政策学部・小論文の問題です。この年は、職場にコーヒーメーカーを置くと生産性が向上する理由に関する文章をヒントとして、年収が上がると糖尿病死亡率が下がるという関係について、相関・因果の関係で考えられる要因間を図示して分析するという問題が出題されました。どちらも疑似相関で、前者については「厳しい上司」、後者については「健康診断受診率」や「食生活」といった要因が第3変数の一例としてあげられます。この問題を、グループワークで解いてから、これを自分たちの研究結果でやってみようと提案します。

手順としては、最初にグループワークで疑似相関クイズというものを行います。例えば、消防車が出動すると火事が大きくなる、暴力シーンを見ると非行に走ってしまう、アイスが売れると水死者数が増えるというような例を生徒たちに書き出してもらい、「これ実は入試問題にも出たんだよ」と言って、慶應の問題を解かせました。
これを試した後に、「じゃあ人の意見に文句を言うのではなく、自分たちの結果を検証し直そう」と提案すると、授業が結構盛り上がります。
一番もっともらしいことを言えた人が優勝というルールで授業を進めました。

グループワークで、生徒たちは生き生きと図を作り、その後、前に出て発表をしていきました。


例えば、「男子よりも女子の方がメークされた顔を好む」という例では、いろいろ調べてみると、こういう図を作ることができました。そして、校則によるわれわれへのイメージ操作がある、メークが主観的か客観的かという問題、メークが主観のものになったら男子の考えも変わってくる、などといった意見が出ました。
そして、「将来的に好みは変わっていく可能性が大きい」という結論に至りました。

こちらは、「家より外での勉強を好む人の方が勉強時間は長い」という例です。生徒たちがいろいろ要因を書き出していったところ、「〇〇予備校にはイケメンが多い」という意見が出てきました。
しかし、実際に考えを進めてみると、「イケメンが多いから〇〇予備校に行って、勉強時間は伸びるけれども、結果として勉強には集中できなくなるため、勉強の質は下がっている」という結論になり、これには私も笑ってしまいました。このように、発表会は大変楽しく盛り上がりました。

生徒の理解度とやる気の理由~「やっぱり統計はおもしろい」
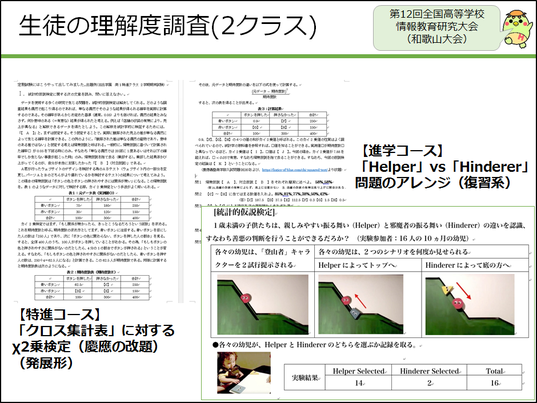
振り返りをきちんと行うという意味で、生徒たちの理解度調査を定期試験で行いました。特進クラスの子たちには、慶應の過去問の改題 (いわゆるχ二乗検定) を出し、進学コースの子たちには、さきほどの赤ちゃんの復習問題を出して、正答率を調べました。
※クリックすると拡大します
仮説を述べる問題は、それなりに正当率が高いものの、どちらのクラスでも有意差が無いことの正しい解釈に関する問いの正答率は低いです。偶然対必然の戦いだと言っているのですが、検定の非対称性まではやはりまだ少し難しいのかもしれないと感じました。ただ、相関と因果の違いを記述しなさいという問いには、8割以上の生徒が正解できています。

また、進学クラスの方で、先ほどの赤ちゃんの善悪区別問題をアレンジして、新たに作った問題を出しました。確かに四角をよく選ぶ、ということで有意にはなったものの、この結果だけで、本当に「赤ちゃんは善悪の判断ができている」といえるのかという問題です。第3の変数を見つけてそれを排除する実験までやりなさいというような記述問題を出したら、きちんと、「色が要因として効いている」とか、「形が要因として効いている」など、対照実験の提案まで含めてしっかり書いてくれました。

進学コースの生徒たちも、正答率が7割近く出たので、第3変数を見つけるという授業をグループワークでやることには、意味があるように感じました。
最後に、生徒アンケートの結果をご覧ください。特進と進学で平均点を見たときに、ちょっと点数が違うから優秀だと言えるかどうか、という質問をしてみました。
「いや、ちょっとそれおかしいんじゃないの」と言って、「仮説検定の仕組みで説明することができるよ」と答えてくれた生徒も結構いました。本当にできるかどうかは置いておいて、疑うことができたというのは大事なことだと思います。
授業の5段階の自己評価を見てみても、講義にせよ実習にせよ、興味関心がずっと削がれないまま進行していたことを、データから読み取ることができました。実際、生徒たちも生き生きと、最後まで取り組んでいたよう見えました。

最後に、生徒には自由記述をさせました。
「情報リテラシーは、情報をむやみに疑うことではないと実感した」という感想が出たのは、嬉しくもあり、また良い言葉だなと思いました。いわゆるデータサイエンスにおける仮説検定や、相関・因果の見極めという練習が、まさにその疑うコツを見極めるという、情報科の目標の一つになっていくのではないかと感じました。
もう1つ紹介する感想は、長いですが「カラオケに行ったとき、ピアノを習っている子の方が歌はうまい気がするので、今度、ピアノを習っている人と習っていない人について有意差を調べたい」という内容です。カラオケで、国歌を歌ってもらい、その得点を使って仮説検定を行い、有意差があったら自分の子どもにはピアノを習わせることにします、という締めくくりでした。
こういうふうに、日常の中に仮説検定の考え方を応用できる段階にまで至れれば、統計学習の価値も生徒たちの中で高まるかと思います。

私自身、この授業を通して、改めて統計は非常に面白いという感想を持ちました。自分が知らないことも様々に出てくるし、生徒のアイデアも、この通り面白い。情報Iと情報IIが始まるまでに、いろいろな内容を見つけることができたらいいと考えています。
第12回全国高等学校情報教育研究会全国大会(和歌山大会)より