事例141
情報Iを見据えた“情報科”統計教育
日出学園中学校・高等学校 武善紀之先生

先日、今年8月の全国高校情報教育研究会で発表した統計授業の発表(※1)について「ぜひ神奈川でも」という嬉しいお声がけをいただきました。せっかくなので全高情研+αの内容で、本日の発表は作ってきました。
(※1)「高校生が楽しく学べる仮説検定と相関・因果~シミュレーションから始まる『情報科』統計教育」第12回全国高校情報教育研究会全国大会
https://www.wakuwaku-catch.net/jirei19136/
従来のアンケート実習に仮説検定を導入する
教科「情報」でデータサイエンスを扱う単元は、新学習指導要領で言えば、情報Ⅰの「(4)情報通信ネットワークとデータの活用」と、情報IIの「(3)情報とデータサイエンス」になりますが、学習指導要領を読むと、内容は大きく3つに分かれると考えています。
1つ目が自分たちでアンケート集計や分析などの実習を行う内容、2つ目がデータベースやDBMS (DataBase Management System)を扱う内容、そして3つ目が大規模データの分析や可視化といった、いわゆる機械学習的な内容です。今回の発表では、この1つ目の実習について注目しています。

本校の「アンケート実習」は、以前には統計グラフの作成を行っていました。この実習では自分たちでアンケートを作って調査を実施し、集計してグラフを書いて、1枚のポスターにまとめます。
例に挙げた班は、「ひとり〇〇(ex.カラオケ)」に注目して調査を行い、「男子と女子では、女子の方が勇気がある(ひとり〇〇によく言っている!)」と主張するポスターを作っていました。この実習は面白かったのですが、本当に男女で差があるのかどうか、調査結果から偶然性を排除することができていません。そこで、仮説検定をやってみた、というのが全高情研での発表でした。

新学習指導要領の「情報Ⅰ」にも、「データの傾向について評価するために仮説検定の考え方を取り扱うことも考えられる」と書いてありますので、この点はズレてないかな、と考えています。
実際にはイチからデータサイエンスの授業を始めるのではなく、既存のプレゼン実習を改良する形で実習をやってみました。今まではテーマを決めて、アンケート集計をして、プレゼンのスライドを作って、発表するという流れでしたが、自分たちで分析した結果を、仮説検定も含めて、「本当にそうなの?」と戻って戻って、3回疑ってみる、「統計調査3つの疑い」という構造にしたのです。
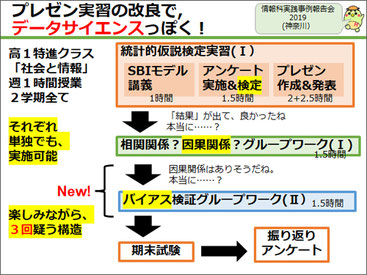
「統計調査1つ目の疑い」として、まずアンケート集計の際に検定作業を持ち込みました。この検定が、今までなぜ難所だったかと言うと、メカニズムと計算が非常にややこしいからです。
数式を使わずに仮説検定の「難所」を切り抜ける
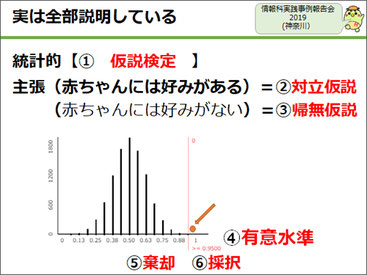
仮説検定のメカニズムを簡単に説明すれば「差がない」という帰無仮説を最初に設定し、いろいろ面倒な計算をして検定量を求め、その検定量をもとに帰無仮説を棄却し、対立仮説(差がある)を主張するというものです。しかしこの「流れ」も「計算」も生徒に理解させるには難しすぎると、ずっと頭を抱えていました。
そんな時に江戸川大学の研究会でJimmy A. Doi先生がご紹介されたSBI (Simulation Based Inference) という方法に出会いました。私もこれを使ってみたら、生徒の理解がかなり良かったので、この場でご紹介したいと思います。

最初に仮説検定とは何かをざっくり説明します。ギャンブルに参加するとき、いきなりゲームに参加するのでなく、まずコインをチェックさせてもらいます。
そして50回投げたら、表と裏が25回ずつ出るくらいでなければおかしいですよね。それでも、表が24回だったり22回だったりすることはあるかもしれませんが、さすがに表が2回だけだったらこのコインはインチキだ、このゲームには参加しない、ということになりますね。「差がない」仮説を設定し、実験をして、ありえないことが起きたら、「差がある」と主張する。仮説検定とはこういうことだよ、という説明をします。

この後でJimmy先生が提示されていたのが、「Helper vs. Hinderer」という心理実験です。
「お助けマン(Helper)と邪魔マン(Hinderer)という二つのキャラクターの動画を赤ちゃんに見せた後、お助けマンの形と邪魔マンの形を見せて好きな方を選ばせると、赤ちゃんは16回中14回お助けマンの方を選びました。ということは、赤ちゃんは善悪の区別がついています」という実験の結果を示します。これに対して、「赤ちゃんに善悪がわかるわけがない」とか「適当に決まっている」という反論が当然出てきます。
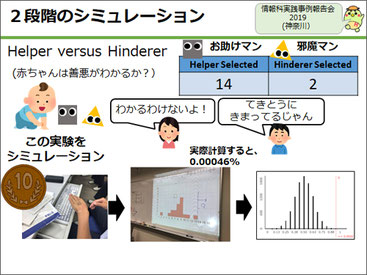
では、赤ちゃんが本当に適当にお助けマンが好きで選んでいるのか、というシミュレーションをしようということで、10円玉を配って全員にコイントスをさせて、結果のヒストグラム生徒たちの間で作らせてみます。「差がない(適当に選んでいる)」状態を、コイントスで再現するわけです。実際に確率を計算すると、16回中14回以上が生じる確率は0.2%で、まず起きません。ということは、ありえないことが起きたんだねという棄却の流れをやってみせます。
さらにこの後、コンピュータ上で10万通りくらいの試行をシミュレーションしてみると、きれいな二項分布の形になるので、生徒には、けっこうすんなり腑に落ちます。
この流れの中に、仮説検定で教えなければならないことが全て入っています。情報科で仮説検定を扱う目標は、仮説検定の考え方を学ぶことなので、とりあえずここまでで十分かなと思います。そして、この後に自分たちのアンケート調査に入ります。
ただ、実際のアンケート調査では「YesかNoか」「アリかナシか」という2項検定では物足りないので、自分が数学の教員でもあることから、数学Aの知識を使えば何となくわかるものとして、フィッシャーの直接確率計算を持ってきました。これはそれほど難しくありません。クラスでアンケート調査をして、クロス集計表を作ります。
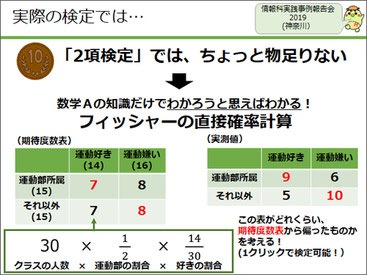
例えば、クラスで運動部所属の人が15人、運動好きな人が14人とすると、運動部所属で運動好きな人の期待値は7人、というのを出すことができるので、この期待値どおりの表と実測値を比較して、実測値がどれぐらいレアかを計算します。
有意差が出なくても自分なりの考察を考える
この計算自体はパソコンに任せてしまえばよく、生徒はメカニズム自体はわかっているので、けっこう楽しく取り組んでくれます。授業自体は、以前のアンケート実習に、仮説検定を加えて実態調査をするという形に少々ひねっただけです。唯一変えたのは、「2×2のクロス集計表に落とし込める形の設問でアンケートをする」という指示を出したことです。調査の自由度が減って不満も出るかなと思っていますが、案外「おかげでアンケートを作りやすくなった」という意見もありました。

これをもとに実習を組み立てると、計6コマで発表まで全部できます。クロス集計は4択で作ることができるので、自分が調べたいことを4択の選択肢にしてGoogleフォームに入れます。これでアンケートをすれば、5分から10分でできます。
この後、自分で手集計をさせましたが、肝心の検定自体には数値を入力すればワンクリックで、有意か有意でないかを判定してくれるサイトもあります。この結果に基づいてプレゼンを作るという流れになります。
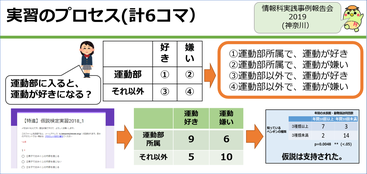
そして、この授業の面白くもあり、難しいところでもありますが、有意差は全員に出るわけではありません。実際、あるクラスでは28人中、有意差が出たのは11人だけで、発表はかなり辛かったかもしれません。ただ、生徒は有意でなかった方が、逆に頑張って自分の仮説を通そうとするので、面白いことをいろいろ言ってくれて、いつものプレゼン実習よりもはるかに発表にオリジナリティーが出たように思いました。
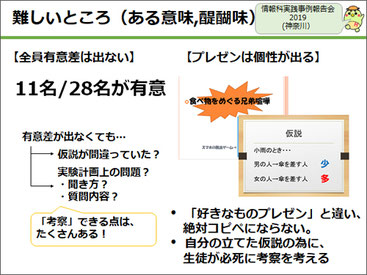
例えば、「食べ物を取り分けるとき、兄弟がいる人の方が、先に取る傾向がある。なぜなら兄弟に先に取られてしまうから」とか、「女の子は、土日はメークをするから、小雨でも嫌なので傘を持ち歩く。だから、男女で傘を持ち歩く頻度が違うのではないか」など、日常生活からテーマを見つけてくることができ、プレゼンの実習としての効果はアップしたと思います。
仮説検定でおしまいにすると、相関と因果の取り違えの危険が…
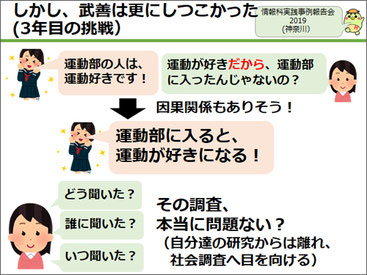
ここまでが1年目の実施でしたが、実は失敗したなと痛感していました。例えばこの実習の発表で、「仮説検定で、運動部に入ると運動が好きになるというということが証明できました」と言う生徒がいました。

検定で証明できたことは、あくまで2変数の連関(相関)のみで、因果関係を説明するものではありません。ですから、「運動部だから運動が好き」ではなく、「運動が好きだから運動部に入った」という逆転関係、あるいは「親がスポーツ熱心だから運動部に入部させて、子どもも運動好きになった」といった「親」という第3変数(交絡因子)が招く疑似相関関係もあり得ます。この違いを意識せずに発表する生徒が多くて、あくまで連関の証明である仮説検定で授業を止めるのはまずいと思いました。

そこで、「統計調査2つ目の疑い」として相関因果の検討をセットで授業に取り入れることにしました。実は、新学習指導要領の情報Ⅰにも、相関・因果・交絡因子の話があるので、ここまで意図されているのではないかと思っています。

入試問題のグループワークで相関と因果の違いを考える→自分たちの調査を見直す
具体的には、ここまでの一連の授業の後に、相関関係か、因果関係かというグループワークを、行いました。解説を30分、ワークを1時間です。
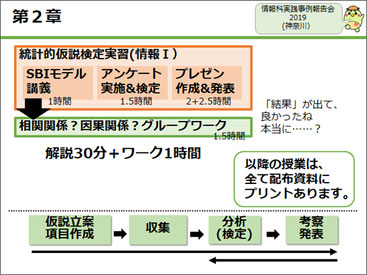
下図の左側が解説に使ったネタは慶應義塾大学(SFC)の入試問題です。「職場にコーヒーメーカーを置くと生産性が向上するから、コーヒーメーカーを置いて仕事の効率をアップしよう」という提案があるメーカーからあったのですが、これは実は疑似相関で、実際は「背景に厳しいリーダーが存在していて、生産性も向上したが、同時にストレスでコーヒーの消費量も増えた」という関係が隠れています。コーヒーの消費量と生産性には、最初に考えた関係はなかった、ということですね。この関係を図示したものをヒントとして、「糖尿病と平均年収」の関係性を図示して答えるという問題でした。
この問題を生徒たちに演習させた後で、「自分たちの研究で、有意になったものに対して本当に因果関係があったのか、見落としている要因や方向性はないか、図示してみなさい」と、4~5人のグループでワークをやってみました。
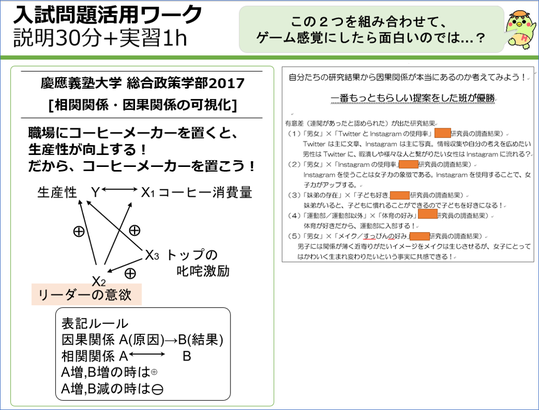
そうすると、けっこうおもしろい結果が出てきました。例えば、「男子より女子のほうがメークされた顔を好む」というものについては、実は男女の差より親からの圧力や校則といった要因が関係していたり、あるいは主観と客観によるメークの違いがあったりしていて、恐らく5年ぐらいで結果は変わるだろう、ということを生徒たちは発表していました。
もう一つ、ネタっぽくなりますが、面白かった例を紹介します。「家より外での勉強を好むほうが勉強時間が長い」という調査が有意になったのですが、これに対しては「自分が外に勉強に行くのは、某予備校にはイケメンがいっぱいいるから」という意見が出ました。勉強の時間は外の方が延びているし、確かに因果関係もあるのですが、「勉強時間は延びてもイケメンに夢中になって、勉強の質は下がっている」と統計調査の結果解釈について、異なる見解が出てきたのです。
バイアスについて考えることで、社会調査の落とし穴に気づく
以上が全高情研で発表した内容です。しかし私はしつこいので(笑)、さらにおまけの挑戦、「統計調査3つ目の疑い」をしました、というのが新しい内容です。「1つ目の疑い」は検定によって、運動部と運動好きに関係があるかを調べることでした。「2つ目の疑い」は図示によって、その方向性やその他の変数の排除を行うことでした。そして「3つ目の疑い」では、その調査はどのように聞いた? 誰に聞いた? いつ聞いた? と突っ込みを続けるものです。その調査自体に本当に問題はなかったのか、という検討を行ったのです。
これはバイアス=偏りという概念で、情報Ⅱで示されています。指導要領では誰に聞いたのか(対象者)という「選択バイアス」、いつ聞いたのか・どう聞いたのか(測定時)という「情報バイアス」が示されており、また公衆衛生などの分野ではこれに加え分析時の「交絡バイアス」などが存在します。

バイアスの具体例として1つ、「脱落バイアス」を紹介します。例えば、「1年後の調査で95パーセントが痩せていた奇跡のジム」があるとします。これは、統計調査上ウソはありませんが、実情はこのようになります。
極端に、ダイエットに対する効果が何もないものだったとしましょう。この時、体重の増減に基づいて利用者をプロットすると初期は、増えた人も減った人も均等に分布するはずです。
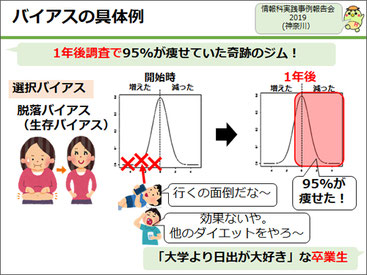
それでも、1年後にその集団はどうなっているでしょうか。当然ながら継続力のない人はジムへ行くのが面倒で途中でやめていったり、あるいは効果がないと感じた人は他のジムへ移ってしまったりしていきます。すると1年後調査では、ほぼ効果があった人しか残っていないことになり、その中での「95%が痩せている」という事実だよね、と言うと、生徒はけっこう腑に落ちるようでした。
ちなみに、脱落バイアスには私もなるほどと思えた例があります。本校の卒業生に、「高校と大学のどっちが好き?」と聞くと「高校、最高でした!」といつも言ってくれて嬉しい、という話を以前から生徒にしていたのです。すると、この授業の後に生徒から「先生のあの話、生存バイアスだよ。卒業後に高校へ顔を見せに来る生徒の多くはそもそも高校を好きなんだから、高校の方が好きだって答えるでしょ」って言われて、確かにそうだな、と。事実かどうかは検証していませんが、可能性はありそうですよね。
「いかにもあやしいグラフ」ではなく、新聞の世論調査を素材にバイアスを見出す
統計実習の最後に、このバイアス検証をグループワークで行いました。本当は自分たちの実習に対して行うことが理想ですが、実習の方法は揃えてしまっています。そこで、最初は「怪しい調査を探してみよう」というテーマを考えました。

しかし以前に、「実際に怪しい調査を探してみよう」というテーマを扱った際、生徒はGoogleで「怪しいグラフ 統計」で検索して、結果どこかで見たようなグラフばかり出てきて終わり、という経験がありました。これではTwitterの面白コンテンツを見て騒ぐことと一緒なので、今回はあえて怪しくなさそうなものを使うということで、新聞の世論調査を使ってみました。
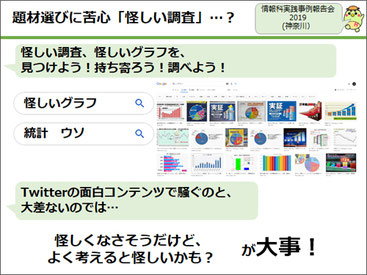
読売新聞は定期的に世論調査を行っています。本校は、読売新聞社が提供する電子ジャーナル「ヨミダスforスクール」を契約しているため、電子ジャーナルからこの調査結果と設問文のセットを作って、これを読ませることを行いました。

読売の世論調査は、誰に・何を・どのように聞いたか、調査票はどう送ったか、回答者の内訳は…など、いわゆるバイアスの検証に必要なことが全て書いてあります。

こういった情報を見ながら、4~5人のグループで「ここにバイアスが掛かっているんじゃない?」「この結果からこの結論を持ってくるのは無理じゃない?」といったことを話し合わせました。そうすると、生徒はけっこう問題点を見つけてくれます。

例えば「選択バイアス」では、「手に取って選びたい本」の調査で、「この調査は郵送法なので、そもそも本に興味がない人は除外されているんじゃないか」とか、あるいは「正確に報じる」という問題の調査で、「『若者はネットの情報にだまされやすい』という結論になっているけど、高齢者はそもそもネットに触れていないから、『だまされたことがありますか』という質問に対しては、『いいえ』と答える率が当然高いだろう」など、細かいところをしっかり指摘しています。これは私としても面白かったです。
アンケート調査実習に対する「3つの疑い」の流れを振り返っておきます。生徒たちは分析結果について検定を用いてその確実性を疑い、考察について相関・因果の検証を用いてその妥当性を疑い、最後に収集プロセスについてバイアスの検証を通して主張の有効性を疑いました。更にこれらの「疑い」に基づいた定期試験と、振り返りのアンケートで、実践は完結させています。
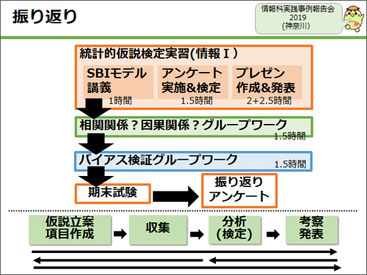
「私たちは今までこういうふうにものを見ていたんだ」という気づき
期末試験の結果からは、相関と因果の関係についてかなり理解が進んだように思いました。他にも、別の解釈や要因を発見する問題の正答率が高くて嬉しく思いました(ただし、これらの結果については検定を掛けていません、申し訳ありません)。
また、お助けマンと邪魔マンでの選択で、お助けマンが14回選ばれた、というのがありましたが、これは形以外にも、色や、形と色の相互作用といった他の要因の可能性もありますよね。
であれば、どういう実験計画を立てれば形以外の要因の影響を除去できるかという、いわゆる交絡因子の排除に関する問題を出したら、これも6~7割は正解できて、概念については身に付けることができたようにと考えられました。
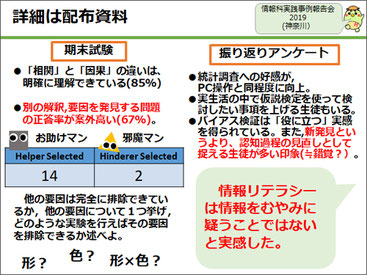
体験型の授業であっても、どうしてもコンピュータを使った実習の方が生徒には人気があるのですが、今回の授業に関しては、コンピュータにあまり触れなくても、「こっちの方が面白かった」という生徒が多くて、嬉しかったです。
また、バイアスの検証は今回初めて行いましたが、他の単元に比べて、新しいことの発見というより、「私たちは今までこういうふうにものを見ていたんだ」といった認知の再確認に関するコメントが非常に多かったように感じました。
また本授業の生徒の感想で、「情報リテラシーは、情報をむやみに疑うことではないと実感した」というものがあり、とても嬉しかったのを覚えています。情報科の中では「SNSは危険だよ、使わない方がいいよ」ではなくて、どう危ないか、どのように防いでいけばよいかを科学的理解に基づいて教えるのが情報科の使命だと、情報モラルの授業も展開されてきたように思います。データサイエンスについても、「正しい疑い方」を科学的理解に基づいて学ぶという使命と意義、そしてその学びを通した本単元の魅力が、このコメントには集約されていると思います。
[質疑応答]
高校教員Q1:質問が2つあります。まず2掛ける2のクロス集計表からできることを調査することで、生徒のほうがテーマが決めやすかったということですが、具体的にどのようなテーマが出てきて、先生はそこで1回チェックをかけたのか、それとも発表までノーチェックで生徒に任せたのかを教えてください。
もう1つは、バイアス検証のグループワークは、どのぐらいの時間をかけられたのかを教えていただければと思います。
武善先生A1:1つ目の質問ですが、まず宿題として2回出します。最初に仮説検定の話をした後に、「じゃあ仮説検定を使って調べてみたいことを見つけよう」ということで、この時点ではフィッシャーの検定のことは教えませんでした。そのため、いろいろなテーマが出てきて、二項検定で済むものもあれば、クロス集計が必要なもの、2×2ではなくて2×3とか、成績の上位・中位・下位のようなものもありました。
ただ、その後にフィッシャーの直接確率計算であることを伝えて、4択問題になるように設問の作り直しの時間を設置しています。ですから、完全に望む形にはならなかったとしても、必ず2×2を落とし込むステップを入れています。ということで、事前にチェックしているかと言えば、そこでチェックは掛けて、集計したGoogleフォームも、一度生徒に配布する前にチェックして、2×2に落とし込めないものは修正させ、再提出させました。
2つ目のバイアスの検証は、実はあまり授業日数が取れなかったこともあって1.5コマ、90分で行いました。0.5コマ(30分)でバイアスの説明をして、授業プリントは「バイアスを打破しよう」という選択バイアスや情報バイアスなどの話を一例ずつ挙げて「こういうものを見つけるんだよ」と説明して新聞を配って、後半0.5コマで書き出しをした後、次の時間で発表をすることを知らせて、残りは宿題にしました。そして、次の時間で0.5コマで発表をしました。
大学教員Q2:先生は数学がバックボーンにおありですが、こういう授業を数学科出身ではない先生方がされるのは、どうすればよいでしょうか。こういう勉強をしたら、といったきっかけを教えていただけたらと思います。
武善先生A2:私のもともとの専門は認知心理学で、人間の脳の神経細胞をシミュレーションするようなことを研究していたので、実はガチガチの理系ではなかったんですね。今回の実践でフィッシャーを使ったのは、数式が一切出てきません。実は、数学科の方にも、統計はとにかく式がいっぱい出てきて、それをいじって終わっちゃうから嫌だ、という方がけっこう多いようです。
その点、情報科はそこをコンピュータに任せることができて、数学科の方が嫌だと言われる部分は解消できると思います。
また、授業が終わった後に、生徒に「この授業を受けて、どの教科と関連が深いと思う?」と聞いてみたら、数学と国語が同数になりました。生徒は、かなり国語的な印象を受けたらしくて、「バイアスの読み取りや相関因果や検定は数字を追うだけではない」と感じるのですね。今回統計を数式を使わずに、ロジックの部分だけ説明するというやり方で切り抜けることが可能だということがわかったので、あまり数学というイメージを持たずにやっていったらうまくいくのではないかと思いました。
※神奈川県高等学校教科研究会情報部会 情報科実践事例報告会2019 口頭発表より












