事例218
「問題解決」の問題解決〜「問題解決」学習を考える
東京都立町田高校 小原 格先生
「情報I」学習指導要領での「問題解決」の進め方

今回は、「『問題解決』の問題解決」ということで、問題解決学習をどのように進めていくかということについてご報告します。
「問題解決」について、高等学校学習指導要領解説「情報Ⅰ」では、「(1)情報社会の問題解決」のア-(ア)で、「得られた情報を文章や図にするなど可視化する」と述べられています。また同じくイ-(ア)では、「思考を広げ、整理し、深め、科学的な根拠をもって物事を判断する」力を養い、その際「問題のゴールを想定する力、複数の解決策を作り科学的な根拠に基づき、合理的に選択する力を養う」とされています。


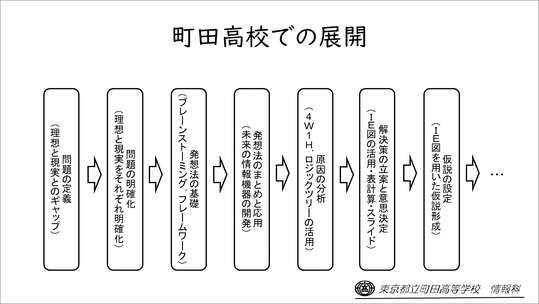
町田高校では、これに則って、問題の定義→問題の明確化→発想法の基礎→発想法のまとめと応用→原因の分析→解決策の立案と意思決定→仮説の設定という流れで問題解決の学習を進めています。
※クリックすると拡大します。
問題解決は、まず「理想」と「現実」の明確化から
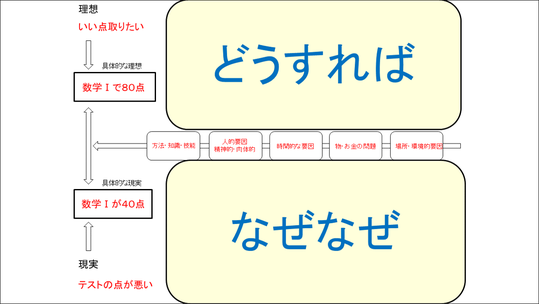
まず「『問題』とは何か」ということですが、ここでは問題というのは「理想と現実のギャップ」とすることにしました。
具体的には、実際には、「朝早く起きたいけれど、実際には遅刻ぎりぎりになってしまう」というのも一つの問題です。このように、生徒たちに「問題というのは身近に非常にたくさんある」ということを意識させてから、身近な問題を発見するところから始めます。
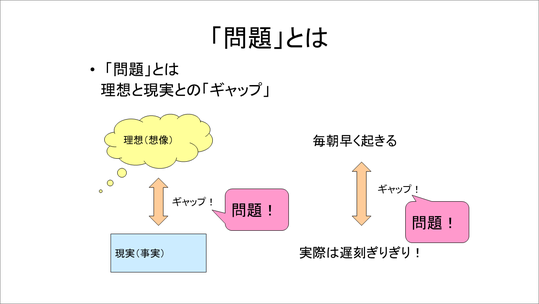
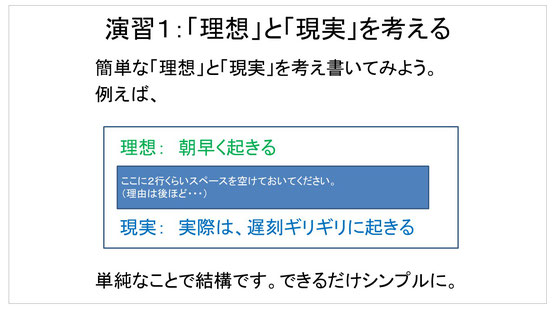
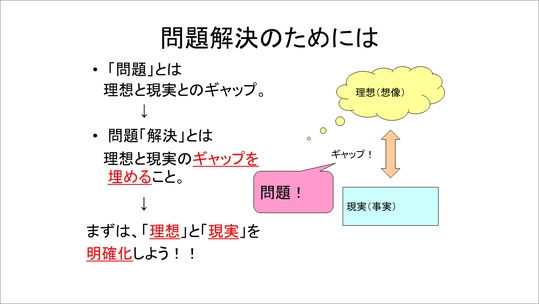
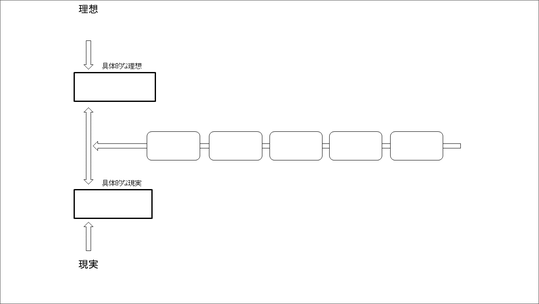
そして、問題を発見したら、今度は問題を解決するというのはギャップを埋めるということだよ、ということを伝え、理想と現実を明確化する重要性について説明します。
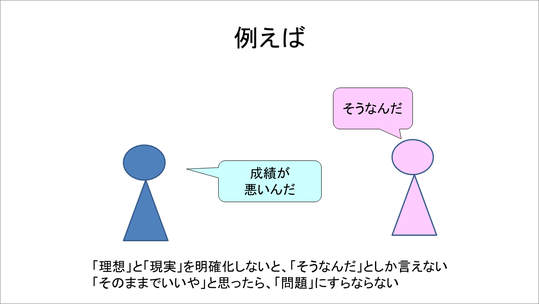
例えば、このスライドで言えば左の人は「成績が悪いんだ」と言いますが、それに対して右の人は、「そうなんだと」しか言えません。なぜなら、理想と現実が明確化されていないので、右の人には、左の人が成績を良くしたいと思っているのか、そのままでいいのかわからないからです。これでは,ここで言う問題にはなりません。
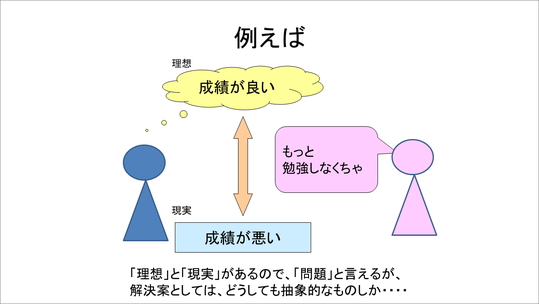
では、左の人が「成績が悪いんだけど、良くなりたい」と言ったとします。確かにこれは対比ができているので、「問題」とは言えそうですが、解決策としては「もっと勉強しなくちゃ」という抽象的なアドバイスにとどまっています。
なぜなら、問題は見えていても、理想も現実も非常に抽象的なため、解決策としてのアドバイスも抽象的なものにならざるを得ません。
そこで、どのぐらい成績が悪いかと言うと「40点しか取れていない」。じゃあ、どのぐらいまで成績を良くしたいかと言えば「80点取りたい」ということにしましょう。
このように、理想と現実を明確化する、できれば数値化することによって、例えば「基礎問題は確実に解こうね。100点取れなくていいのであれば、応用問題も1題は解けるようにしよう」という、具体的なゴールに向けての解決策を立てることができます。

このような形で、具体的な理想と現実を明らかにすることの必要性と重要性を説明した後、スライドの真ん中の部分のように具体的な理想と具体的な現実を記述させ、ペアになって相手に説明する演習も行います。

「フレームワーク」で発想の幅を広げる
次に、より良い問題解決のPDCAサイクルについて説明した後、「情報」の授業で扱うからには、ということで、リサーチの重要性や、情報がどのように生かされるのかということについても説明していきます。
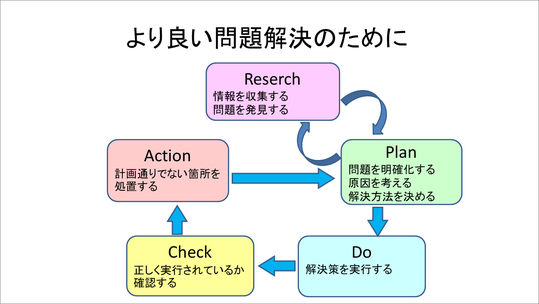
ここで問題解決のために幅広くアイデアを広げるのですが、これがなかなか難しく感じる生徒もいるので、少し視点を変えて、アイデアを広く広げるやり方そのものについても指導していきます。

そこで私が取り入れてるのが、「フレームワーク」です。これは、あえて切り口を設定して、その中で思考することで視野を広げるというものです。
例えば「封筒の使い方にはどんなものがあるだろう」ということで、本来的な使い方以外に、封筒の大きさや形、材質、複数集めたら、など,あえて着眼点を意識的に設けることで発想を広げていく、というものです。

そして、練習問題として「鉛筆の使い道」をできるだけたくさん考えよう、ということを行います。これは生徒全員に当てて、何種類出てくるかを競争させることもあります。

このように、まず頭を柔軟に使うことを行った後、ブレーンストーミングにつなぎます。中には非常に奇抜なアイデアも出てきますが、ここではとにかくアイデアを出すことが目的なので、まずは受け入れていこう、と。特に批判の禁止については、強く指導をしています。こうして生徒同士でブレーンストーミングを楽しく行った後に、「未来の情報機器を考える」の演習を行います。

「未来の情報機器」のアイデアを考え、出て来たアイデアを整理する
まずはブレーンストーミングの要領で、自由に考えてつなげ、それぞれ数人に発表してもらいます。その際、つなげ方の参考として、アイウエそれぞれについて次の要領でコメントし意識させます。

例えば下図のアはIoTのことですね。イは掃除機とカメラのどちらに主眼を置くかによって、できあがるものも変わります。
ウは、洗濯機は水が必要ですが、エアコンは除湿で水が要らなくなります。要るものと要らなくなるものを組み合わせると、エコなシステムができるというものですね。
エについては、10年前には考えられなかったけれど、今は当たり前になっているものです。このように、今はなくても将来できるようになるかもしれないもの、という視点を生徒にコメントし、今後つなげる際の参考としてもらいます。

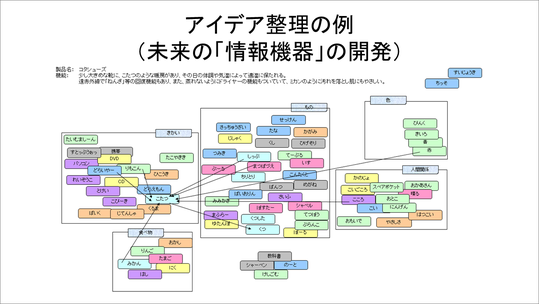
アイデアを整理する方法がこちらです。これをもとに、出て来たアイデアを整理します。

下図は過去の授業で生徒が行ったものですが、この場合は「こたつ」に周りからいろいろな視点から要素を集めて、より面白いもの、ユニークなもの、世の中に役立ちそうなものを考えていきました。
※クリックすると拡大します。
原因や解決方法を考えるための「ロジックツリー」「4W1H法」
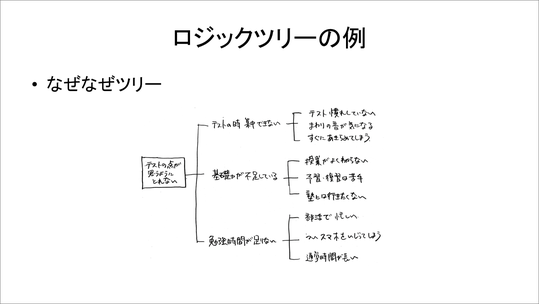
この後、より深めるということに視点を動かします。ロジックツリーの演習をした後に、「4W1H法」を行います。

※クリックすると拡大します。
この「4W1H法」は、Who(人的側面)、When(時間的側面)、Where(空間・環境的側面)、What(物質的側面)、How(知識・技能・方法的側面)からWhy(なぜ)を考えていくもので、フレームワークから派生したものです。
※クリックすると拡大します。
IE図を使って「なぜなぜ」と「どうすれば」を整理する
原因を分析するためのテンプレートとして、私が開発したIE図(※)というものを用いています。

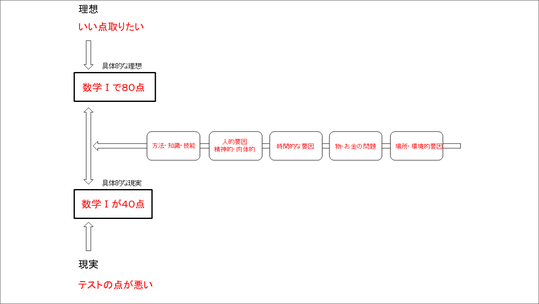
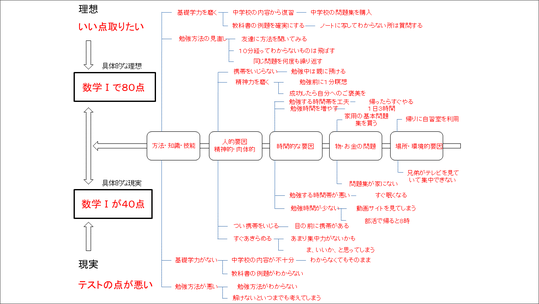
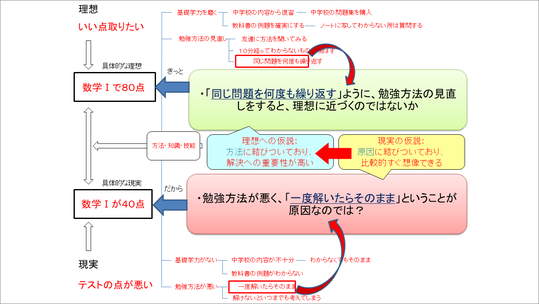
このIE図の左側には、先ほど説明した「具体的な理想」と「具体的な現実」が入ります。
それに対して、4W1Hがあり、なぜ数学Ⅰが40点という具体的な現実になっていくのかというなぜなぜツリーが下段、どのようにすれば具体的な理想である80点に近づくのかというツリーが上段に展開されていく形になります。
※クリックすると拡大します。
※クリックすると拡大します。
具体的にあてはめるとこのような形になります。下の「なぜなぜ」の部分に対応する形で上半分の「どうすれば」が書かれます。問題が見やすく,かつ,その原因と解決策が1枚のページに表現できるため,非常に書きやすく見やすい便利なシートになっています。
※クリックすると拡大します。
最善の解決策を選ぶために座標軸やマトリックスに分類配置する
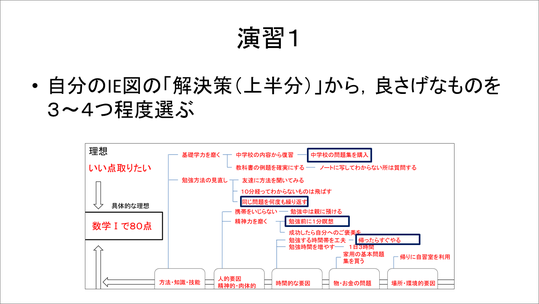
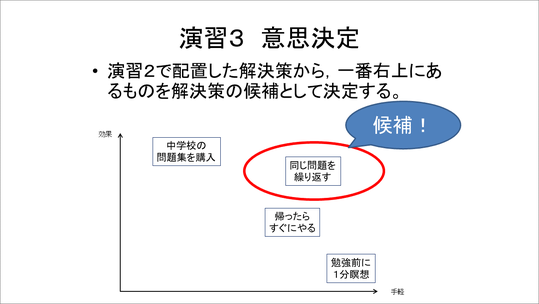
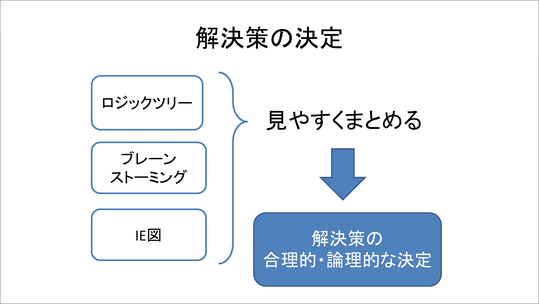
このIE図を用いて見易くまとめることによって、解決策のアイデアが一覧できます。これらのアイデアから、どの解決策を採用するのかという論理的・合理的な意思決定につなげていきます。上段の解決策案から有効と考えられるものをからいくつか取り出して、座標軸やマトリックスに整理します。

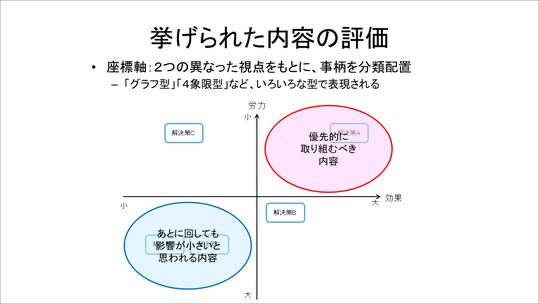
座標軸では2つの異なる視点を軸として、右上に優先的に取り組むべき内容が来るように分類配置します。
例えば、この場合は「労力」と「効果」を2軸として、実際にここに配置しながら右上のものを候補に決めていきます。
※クリックすると拡大します。
※クリックすると拡大します。
このように整理することで、何となく解決策を決めるのではなく、「手軽さと効果に重きを置いて選んだ結果、これが最善の候補として挙げられる」という合理的な説明ができ,説得力を持ってプレゼンテーションを行うこともできます。
※クリックすると拡大します。
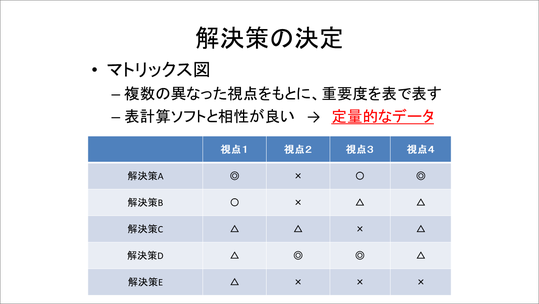
定性的データは、座標軸を使いますが、定量的データはこちらのような表の形のマトリックス図で整理します。これを使うと、複数の異なった視点をもとに重要度を表で表すことができるので便利です。また、意志決定をする際、単なる「多数決」ではなく、例えば、◎は4点、〇は3点、△は2点、×は0点などと点数化し、重みづけをして合計を行うことで、第2希望・第3希望などにも配慮した意思決定ができることにも触れていきます。
この計算式を作成し重みづけした合計を出す作業は、表計算ソフトの使い方の良い演習にもなるので、私もよく使っています。
仮説形成もIE図を使って行う
次が仮説形成(アブダクション)です。実際、仮説を立てるのがなかなか苦手な生徒もおりますので、こちらも先ほどのIE図を基に,合理的な作成方法を指導します。

IE図を作った際に、下段は、原因と考えられるもの、上段には、逆にそれに対する解決策をとにかくたくさん挙げていきました。ということは、実はこの段階で既に仮説ができていることになります。

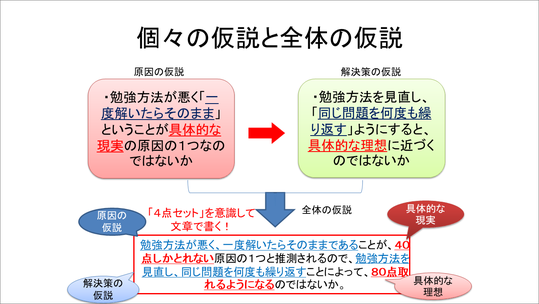
ですから、上段の解決策の仮説、このスライドで言えば「同じ問題を何度も繰り返せば、数学Ⅰで80点取れるのではないか」という具体的な解決策を採用したとすると、それに対する具体的な原因は、下段の「勉強法が悪く、一度解いたらそのままだ」というものに当てはまります。
※クリックすると拡大します。
そこで、この二つを組み合わせると、例えば「勉強方法が悪く、一度解いたらそのまま」というのが具体的な現実の原因であれば、「同じ問題を何度も繰り返す」という解決策を取れば、具体的な理想に近づくということになります。
このような手順を踏むことで、4点セット、つまり『原因の仮説』から『具体的な現実』、『解決策の仮説』『具体的な理想』につながる仮説形成がシステマチックにできるので、生徒の指導が非常にスムーズにできます。
※クリックすると拡大します。

また、この手順を通して、生徒が立てた仮説を検証することで、仮説形成、演繹、帰納、修正と再検討というPDCAのサイクルも説明します。