事例237
数学科と連携した情報の授業実践について
東京都立新宿山吹高校 中山享司先生

東京都立新宿山吹高校の中山です。
下のスライド画面右上のQRコードを読み取っていただくと、今回の発表資料のサイトにジャンプしますので、ご興味があればぜひご覧ください。

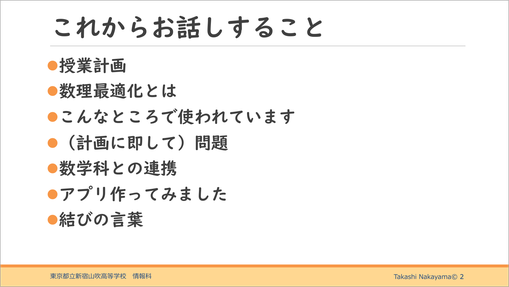
今回お話しすることが、下図です。
まずは授業計画について。そして、数理最適化についてご説明します。そして、生徒が実際にやってみる問題の例。それから、今日のタイトルに挙げた数学科との連携について。そして、その延長でアプリを作ってみたというお話をして、まとめになります。
授業計画~「(3)コンピュータとプログラミング」に入るまでにプログラムの指導を行っておく
早速指導計画についてです。
「情報Ⅰ」の「(3)コンピュータとプログラミング」の「(ウ)モデル化とシミュレーション」での実習を想定したものをご紹介します。
これに当たっては、指導の効率を上げるためにできるだけ「(1)情報社会の問題解決」と「(2)コミュニケーションと情報デザイン」の授業の中で、例えばGoogle Colaboratoryなどプログラミングをするソフトを立ち上げたり、基本的な入出力や四則計算などまでを、毎回5~10分程度のプログラミングで習得しておくのが良いと考えています。
※クリックすると拡大します。
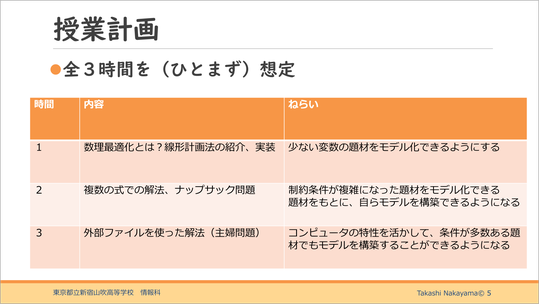
授業計画としては、ひとまず3回を想定しました。なぜ「ひとまず」なのかは、後ほど述べます。ここでは、「モデル化ができるかどうか」ということがとても大切です。
※クリックすると拡大します。
数理最適化~現実の問題を数理モデルとして定義する
数理最適化とは、現実の問題を数式として定義し、さまざまな制約条件を満たしながら、コストの最小化や利益の最大化などを行うものです。
数式で表したものを「目的関数」といい、変数にどのような組み合わせや値があるかを求めます。

先生方は、こんな会話を聞いたことはないでしょうか。例えば、数学が苦手な生徒は、数式モデルと言われてもよくわからないとか、現実の生活と関係ない、といった拒否反応を示すこともあるかと思います。

そんな生徒たちに少し喝を入れ、「この世は数理最適化だらけなのだ」と。「世の中は数理最適化で成り立っているんだよ」と言ってしまおうと思います。
ここから具体例をお示しします。
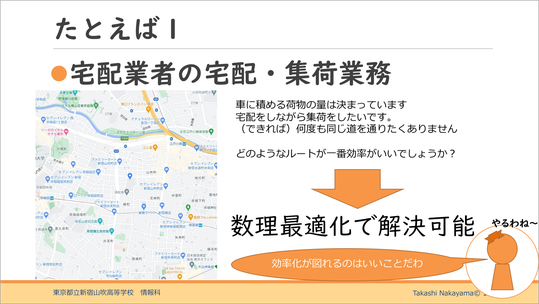
例えば宅配業者の宅配・集荷業務です。
車に積める荷物の量は決まっていますし、宅配をしながら集荷もしたい。さらに、宅配や集荷の際には、できるだけ道を戻ることなく一度に回りたいものです。
数理最適化では、この効率化を図ることができます。
※クリックすると拡大します。
また、アルバイトのシフトを組むのはとても大変です。
従業員ごとに、特定の曜日や時間帯でなければ出勤できない、専門の契約業務でないとダメ、といった個々の事情があります。
それを鑑みながら、その日ごとに必要な従業員数を確保するという難しい問題も、数理最適化で解決可能です。高校生の皆さんも、こんな場面で数理最適化にお世話になっているかもしれません。
※1「勤務シフト作成お助けマン」
※クリックすると拡大します。
他にも、タクシーの配車計画があります。
週末、なかなかタクシーがつかまらないことも数理最適化で解決可能で、待ち時間をほとんどなくすことができます。ただこの場合は、主語が違うところがポイントです。「週末はなかなかタクシーがつかまらない」という時の主語は利用者ですが、数理最適化で解決可能で配車の最適化ができるのは、タクシー会社が主語になります。
では実際に問題をやってみましょう。
実際に最適化をやってみる
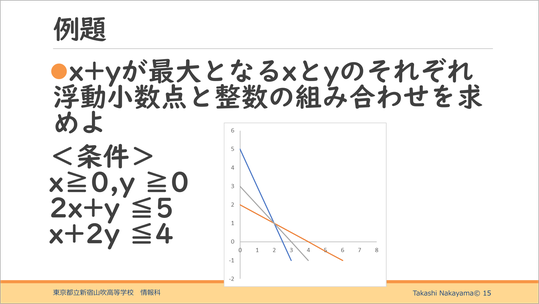
これが1時間目で扱いたい問題です。よくある線形計画法の問題です。詳しい数式は、ここでは重要ではありません。
この線形計画法は中学卒業程度の知識があれば充分取り組めると考えています。
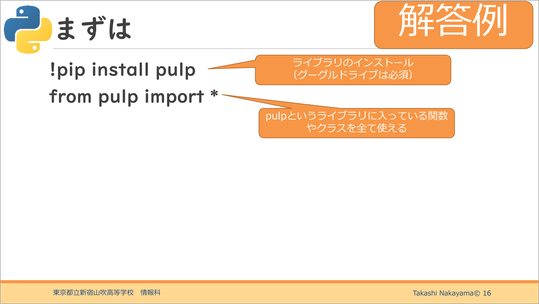
ここではGoogle Colaboratoryが必須となります。ライブラリをインストールし、pulpを使います。このpulpに入っている関数やクラスは、全て使うことができます。
※クリックすると拡大します。
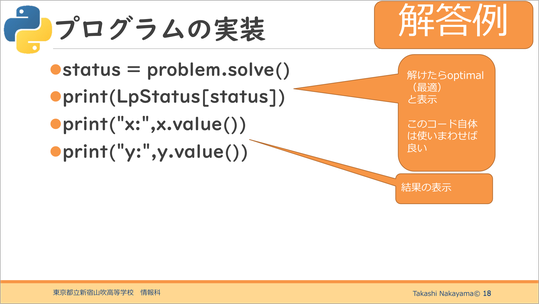
プログラムの実装に入ります。
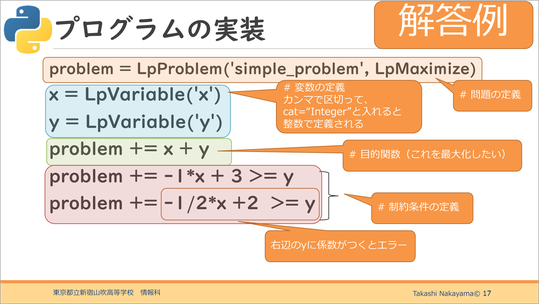
数理最適化のプログラムの場合、必ず書かなければならないことが4つあります。
1つめが問題の定義。次に変数の定義。3つめが目的関数。最後が制約条件の定義です。
今回の問題ではx+yが最大となる組み合わせを求める最大化問題なので、最大化を求めるLpMaximizeを使います。
※クリックすると拡大します。
最小値を求める場合はLpMinimizeを使います。ここは定型文なので、生徒はメモ帳にコピーしておいたものを使わせる形でよいと思います。
こうすることで、コンピュータが計算して、答えを表示してくれます。
※クリックすると拡大します。
指導のポイント~なぜ線形計画法を使うのか?
指導のポイントです。
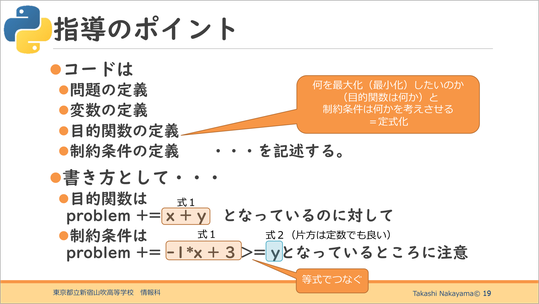
コードには、問題の定義、変数の定義、目的関数の定義、制約条件の定義の4つを記述する必要があります。
この「目的関数の定義」と「制約条件の定義」がよく考えるべき部分で、先生としても、生徒に考えさせて解きやすくなるように誘導する仕掛けが必要だと思います。
書き方の特徴としては、目的関数は「problem+=」で式が1つだけなのに対し、制約条件は「problem+=」に式が2つあります。この2つの式の間に「=」などがあってつながれており、もう片方は定数でもよい、というのが制約条件の書き方です。
このように、簡単な問題でまず書き方を学ぶことがスタートになります。
※クリックすると拡大します。
ではなぜ線形計画法を使うのか、ということについて。
まずは身の回りのことを抽象化できるようにしたい、ということがあります。
このときにモデル化、抽象化したもの数式の解法を線形計画法で表わすと、意外にたくさんのことが解決できます。それが線形計画法を扱う理由です。
どのようにしたら抽象化できるのか、どうしたら式にできるのかということを、考えさせるのがポイントです。
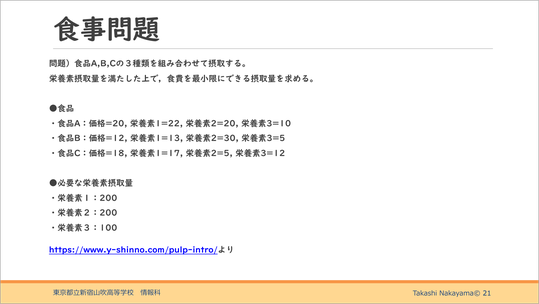
次は、「食事問題」です。
食品A、B、Cの3種類を組み合わせて摂取するとき、栄養摂取量を充たした上で、食費を最小限にできる摂取量を求めるというものです。こんなこともコンピュータを使えば簡単にできます。
こちらが解答例です。今回は価格の最小値を求めますので、先ほどはMaximizeだったところをLpMinimizeにします。
※クリックすると拡大します。
大事なのがここからです。一番上の行が目的関数、その下3行が制約条件です。この問題を式にしましょうといったときに、目的関数はどのように書いたらよいのか、制約条件はどのように書くのか。
この答えに至るまでの誘導をどのように行うかをいろいろ考える必要があると思います。
※クリックすると拡大します。
次は「ナップサック問題」です。
宝島で手に入れたお宝をリュックに入れて持ち帰ろうとしたが、リュックには65㎏までしかお宝を詰めることができない。うまくお宝を選んで、利益が最大になるようにするには、どのような組み合わせにしたらよいか、というものです。
ここではそれぞれのお宝は一応無限にあるということにします。
この問題を見て、ある生徒が「こんなの、何回も宝島に行けばいいじゃん」などと言われましたら、一度島を出たら戻ることはできない、と返答してください。
※クリックすると拡大します。
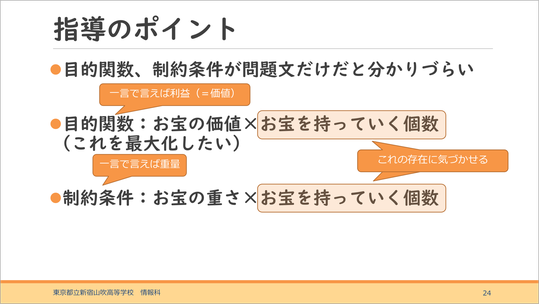
この問題を初めて見たときは、私は全然解けませんでした。なぜかと言うと、問題文だけでは、目的関数と制約条件がわかりづらいためです。ですから、ここは少し丁寧に解説したほうがよいと思います。
お宝をたくさん持って帰って多くの利益が出るようにという目的関数は最大化したい。それどのように求めるのかというと、「お宝の価値×お宝を持っていく個数」の存在に気付かせなければなりません。制約条件は、全部で65㎏までしか持って帰れない点ですが、数式で65㎏をどう表現するのかという問題になります。
お宝の重さと個数を掛け合わせたものの必要性に気づかせる、ということが指導のポイントではないでしょうか。
※クリックすると拡大します。
こちらが解答例です。コードが細かくなっていますが、ポイントは「lpDot」で、内積を取ってくれるという、とても便利なものです。
例えば上から5行目に、「problem+=lpDot(values,amounts)」とありますが、こちらを解説します。
まず、amountsという変数は、お宝を持っていく個数で、valuesが価値です。つまり、(values)105の価値のもの、(amounts)それを何個か。140の価値のもの、それを何個か。65の価値のもの、それを何個か…ということを、それぞれ105×(105のお宝の)個数、140×(140のお宝の)個数、65×(65のお宝の)個数の内積を取って、それを全て合計したものを出してくれます。
その下の「lpDot(weights,amounts)」が重さです。10キロ×(10キロの)個数、13キロ×(13キロの)個数、6キロ×(6キロの)個数が出せて、これの内積を全部足したものが65キロになるようにしてくださいと書いて実行すると、すぐに結果が出てしまいます。すごいですね。
※クリックすると拡大します。
コンピュータを使うといろいろな組み合わせが考えられ、それらを試行できます。
数字を変えればやり直すことも可能で、これがモデルを作るメリットです。ここまでできれば、かなりの数理最適化の達人と言えますので、身の回りのことを題材にして問題を作らせるといった活動をするとよいと思います。
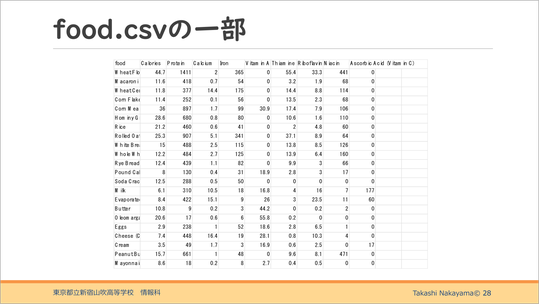
こちらの「主婦問題」はおまけで、csvファイルを使った問題もできるという一例です。
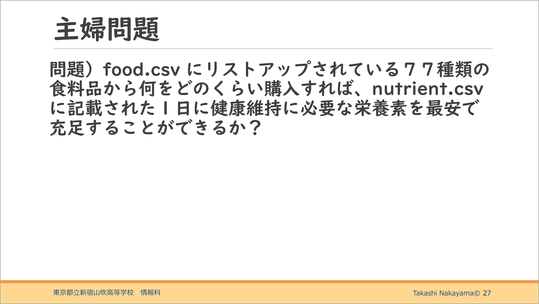
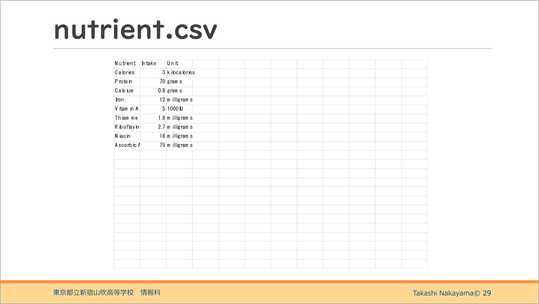
このような外部ファイルを使って、77種類の食料品から何をどのくらい購入すればnutrient、つまり栄養素に記載された、1日に健康維持に必要な栄養素を最安で充足することができるかということです。
※クリックすると拡大します。
※クリックすると拡大します。
この辺りは下準備で、5行で出てしまいます。先ほどのナップサック問題ができていれば、その応用というレベルです。
※クリックすると拡大します。

※クリックすると拡大します。
こんな応用も可能に
例えばこんな問題が作れます。
スムージーを作るのに、栄養は取りたいけどカロリーは取りたくない。バナナ、トマト、きゅうりなど、スムージーに使われる食品の栄養表を用意して、問題を作らせてみてはどうでしょう。
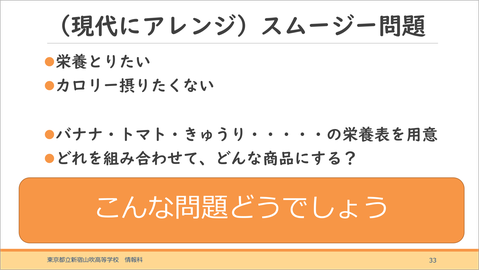
指導のポイントは、数理最適化の問題全体をつかんだ問題を定式化し、目的関数と制約条件を作る定式化。式を作るイメージを持てるかどうかが勝負です。
文章題の文書を読んで式にする力をぜひ身に付けてほしいです。

数学科とどう連携する?
さて、数学科の連携については、なかなか勇気のいるところです。
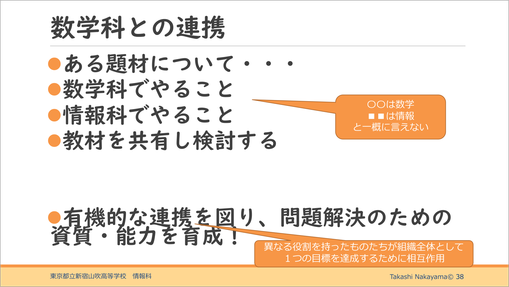
ある題材について、数学科でやることと情報科でやることのすみ分けを、教材を共有してお互い検討し合うことが重要だと考えます。決まりもないので、話し合いを通じて総合的に生徒の問題解決のための力を付けていこうとすることが大切です。
生徒にとっても、幅広い教養を身に付けられるという部分が最大のメリットであると思います。「情報」の時間のみでは、どうしても狭く限られた内容になってしまいますが、「数学」と「情報」のように、複数人で協力して指導することで、1人では扱えないところまでカバーする指導が可能だと思います。
※クリックすると拡大します。
さて、次はアプリ(※3)を作ってみたことのご報告です。
これは、会計時に硬貨を「なるべく少ない数で払う」「なるべく多くの数で支払う」ことを計算するアプリです。
支払いの金額とお財布の中に入っている硬貨の枚数を入力し、「最小化」というボタンを押すと、今持っている硬貨を使って620円を支払うために、一番少ない枚数の組み合わせを示してくれます。
また、お財布の小銭が多くなってきたのでより多く使いたい場合は、「最大化」を使って620円払うのに500円玉を持っていても使わずに、20枚の硬貨で支払うというようなものです。こんなアプリを作ることができます。
※3 https://coin-problem.herokuapp.com/
コンピュータが普及した現代においても必要な力を身に付ける
まとめです。
当初は3時間の指導計画を考えましたが、自分で問題を作らせるという活動を入れた場合、3時間ではなく5時間程度は必要だと思います。
そして身の回りのことを抽象化、モデル化して問題解決する力は、コンピュータがこれだけ普及した現代においてとても必要です。
ですから、少し難しいかもしれませんが、様々な教科の先生がたと協力しながら学校全体で生徒を指導していくような活動がよいと思います。

第15回全国高等学校情報教育研究会全国大会(オンライン大会) 分科会発表より