事例267
大学入学共通テスト試作問題「情報I」第3問の解説指導
東京都立新宿山吹高校 中山享司先生
※中山先生の動画はこちらをご覧ください。

この発表は、授業でプログラムを学習したけれど苦手意識を持ってしまった人や、そもそも「情報」がよくわからないから入試対策を諦めようとしている人に踏みとどまってほしくて作成しました。この発表を見て頑張ってみようと思っていただけたら幸いです。

今回解説する令和7年度大学入学共通テスト試作問題「情報I」(※1)の第3問は、問題文とコードが短いのが特徴です。問題の検討をしていきますので、問題をお手元に置いてご覧ください。
問1 最小交換硬貨枚数を求めるプログラムを作る~関数の作り方を確認しよう
第3問、問1です。
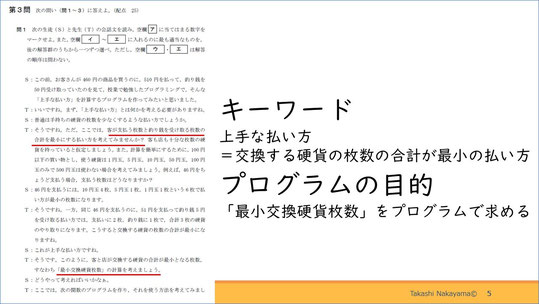
この問題は、上手な払い方、すなわち最小交換硬貨枚数を求めるプログラムを作るというものです。
※クリックすると拡大します
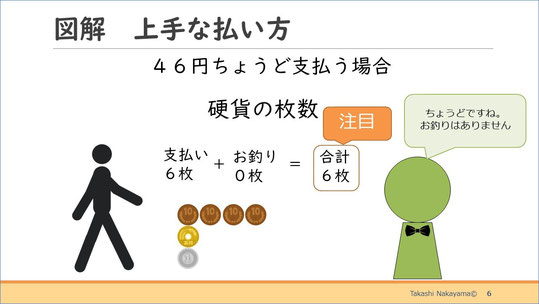
上手な払い方についてイメージで確認しましょう。まず、価格が46円のものに対し、46円ちょうど支払った場合です。この場合は、支払いに6枚、お釣りに0枚で、合計6枚の硬貨が交換されます。
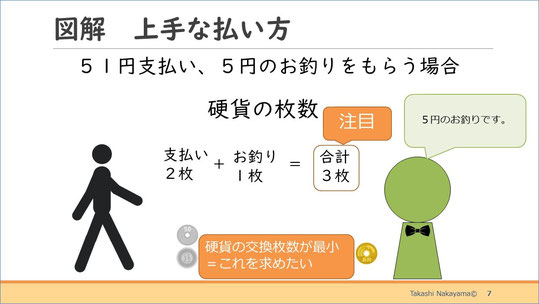
次に、51円支払い、5円のお釣りをもらう場合です。この場合は支払いに2枚、お釣りに1枚で、合計3枚の硬貨が交換されます。
このような、硬貨の交換枚数が最小の支払い方をプログラムで求めていくというのがこの問題のテーマです。
問題の解法に入る前に、この問題で出てくる関数と、それに関わる用語の確認をします。
この問題は関数が使われていますので、表記等についてここで正しく理解しましょう。

まずはスライド左下の用語です。
「関数」とは、データを受け取り、何かしらの処理を行い結果を返す命令のことです。「引数」とは、関数に渡すデータのことです。「戻り値」は、関数が処理をした結果のことです。
では、これらの用語をイメージと共に確認します。スライド右下の図を見てください。
8円というデータを関数に与えます。そうすると、関数が5円玉1枚と1円玉3枚が最小の組み合わせであることを調べてくれます。そして、この組み合わせは硬貨4枚であるということで、4という数字を出力します。このとき、8円という関数に与えるデータを引数、関数から出力された硬貨の枚数である4を戻り値といいます。
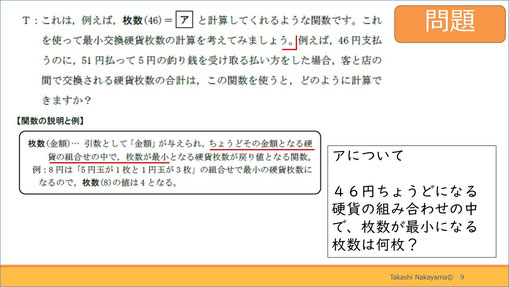
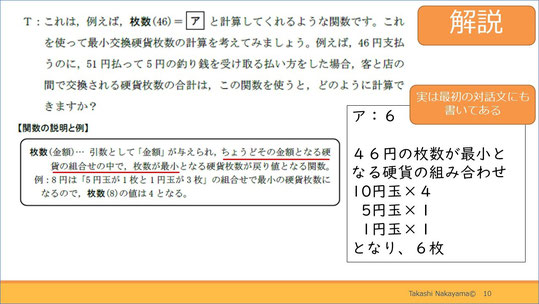
その上で、左上の関数の説明と例を見てみましょう。枚数(金額)は、引数として金額が与えられ、ちょうどその金額となる硬貨の組み合わせの中で、枚数が最小となる硬貨枚数が戻り値となる関数です。
例えば、8円は「5円玉が1枚と1円玉が3枚」の組み合わせで最小の硬貨枚数になるので、枚数(8)の値は4となります。
では、問題の検討に入ります。まずは問題文を確認してください。
「ア」は、先ほどの関数の説明を理解すれば正解できる問題です。右下のヒントを頼りに解いてみてください。
※クリックすると拡大します
解説です。答えは6です。
46円の枚数が最小となる効果の組み合わせに必要な枚数を答えればOKです。
※クリックすると拡大します
次は「イ」です。
解答群の表記には思わず怯んでしまいますね。ここは落ち着いて、何を聞かれているのかを把握するために下線部を確認します。次に右下のヒントを参考に答えを検討します。迷ったら四つの選択肢それぞれについて合計の数値を求めてみましょう。
※クリックすると拡大します
解説です。答えは「0」です。
51円払って5円の釣り銭を受け取る際の合計枚数ですので、それぞれの金額を引数にすればよいでしょう。この関数の表記に面食らってしまうことも想定されますので、ぜひ繰り返し取り組んでください。
※クリックすると拡大します
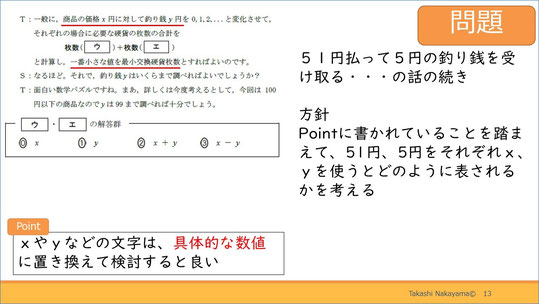
次に「ウ」「エ」ですが、この設問は少し難易度が高いと思いました。というのも、XやYといった文字が出てくるからです。
このようなときは、具体的な数値に置き換えて検討するとよいです。それを踏まえて検討するのですが、この設問は51円払って5円の釣り銭を受け取る払い方の話の続きです。それでは、右側の方針を参考に解いてみてください。
※クリックすると拡大します
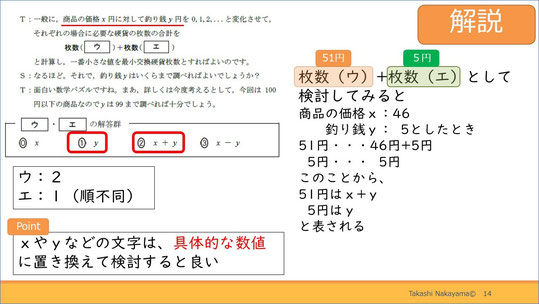
解説です。答えは「1」と「2」です。
51円と5円をそれぞれXとYを使って表すと、簡単に正答にたどり着きます。左下にあるとおり、XやYのように文字で表されていてよくわからなくなったら、具体的な数値で検討するのがポイントです。
※クリックすると拡大します
問2-1 まず何をしたいのかを問題文から把握した上で、剰余算の割り算でできることを考える
続いて問2「オ」「カ」です。
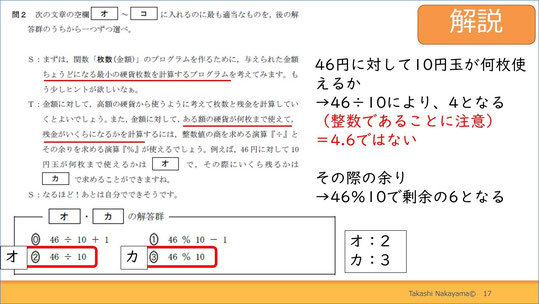
下線部を確認し、まず何がしたいのかを把握します。その上で、余りを求めるいわゆる剰余算の割り算でできることは何なのかを考えてみます。また、解答群を見ると、+1や-1があったりなかったりしていますので、このような時は選択肢を実際に計算してみるとよいでしょう。
※クリックすると拡大します
解説です。答えは「オ」が「2」、「カ」が「3」です。実際に計算してみると正答できます。
※クリックすると拡大します
問2-2 変数と配列の違いをイメージする
それでは、続きです。
ここではまず、問題文と配列について確認しましょう。
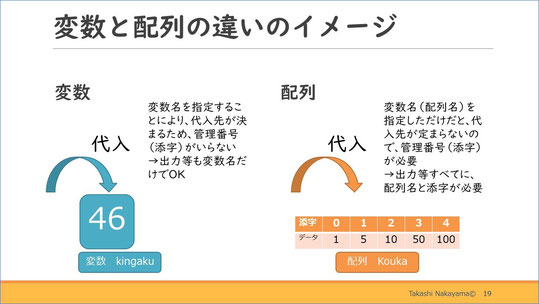
ここで配列が出てきたので、配列と添字について確認です。右に書いたとおり、配列とはデータを格納する連結した箱、添字とは、連結した箱それぞれに付いた管理番号というイメージを持つとよいでしょう。
※クリックすると拡大します
もう少し詳しく見てみます。
これまで数値の格納に使用してきた変数は、変数名を指定すれば代入先や出力元がわかりました。
しかし配列は、配列名を指定しただけだと、連結したどの箱に代入するのかが定まりません。そこで、この場所に代入や出力ということをきちんと指定するために、添字が存在すると思ってください。
※クリックすると拡大します
それでは、図1のプログラムについて検討していきます。
まずはプログラムの1行目から見ていきます。配列のKoukaに、1円から硬貨の額が小さい順に格納されています。入れています。
※クリックすると拡大します
2行目は46円について検討するということで、kingakuという変数に46を代入しています。
3行目は、硬貨の枚数を管理するmaisuという変数に0を代入しています。これは、今後このmaisuという変数に値をどんどん加算していくため、初期値をここで設定しています。初期値をなぜ設定するのかについては、後ほど解説します。
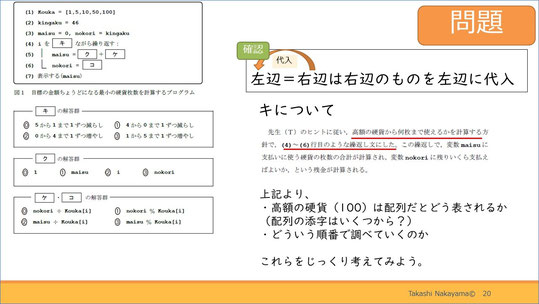
そして、nokori=kingakuという表記ですが、ここは注意が必要です。プログラムでは「=」(イコール)と書いた場合、右辺のものを左辺に代入するという意味になります。ですので、これまでも「=」が使われていましたが、これは数学のような「同じ」という意味ではなく、「代入する」という意味であるというところを注意しましょう。
いよいよ問題の4行目ですが、iを「キ」しながら繰り返す、とあります。どのような方針で繰り返すのかは先の問題文にあったので、下線部を中心に確認してください。
それでは、右下のヒントを参考に考えてみましょう。
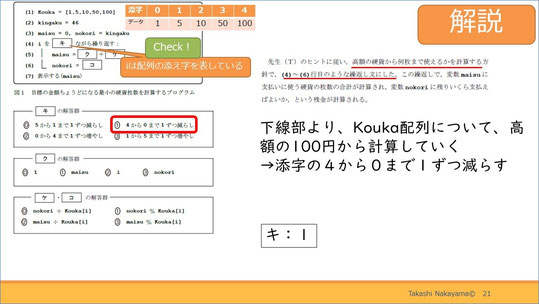
解説です。答えは「1」です。
iは配列の添字を表しています。繰り返し文では「iと言ったら配列の添字を表す」というのはよくある表記の仕方ですので、併せて覚えておきましょう。
そして問題文より、100円から何枚使えるか計算していきます。100が格納されているのは、Kouka配列の添字4のところです。そして、1が格納されている添字は0です。そのため、4から0まで1ずつ減らすという選択肢が適切です。
※クリックすると拡大します
問2-3 どのようにしたら支払いに使う枚数が追加されるか考える~数学とは異なる表記に注意!
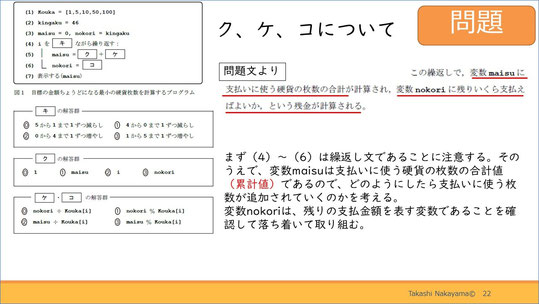
続いて、5、6行目「ク」「ケ」「コ」についてです。これは問題文から何をしたいのかを確認するところから始めます。
どうやら変数maisuは支払いに使う硬貨の枚数の合計であり、変数nokoriは残りいくら支払うのかということを表しているようです。ここで押さえておきたいのが、4から6行目は繰り返し文であるということです。
つまり、100円が何枚使えるのか、使ったら残りいくら支払うのか、そして次に50円、10円から1円まで全て調べます。このことを踏まえて、右下のヒントを参考に考えてみてください。
※クリックすると拡大します
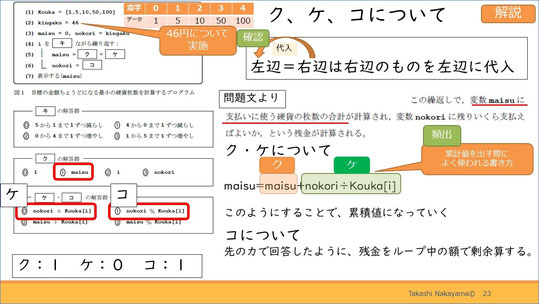
解説です。答えは「ク」が「1」、「ケ」が「0」「コ」が「1」になります。
特に注意したいのが「ク」と「ケ」です。スライドにもあるように(maisu=maisu+nokori÷Kouka)のような、左辺にも右辺にも同じ変数がある表記は、数学では見慣れない書き方で戸惑うこともあるかと思います。プログラムでは=は右辺を左辺に代入ということを、併せて確認しましょう。
その上で、繰り返し文の問題攻略法をお伝えします。
※クリックすると拡大します
問2-4 繰り返し分の攻略法=値の変化をトレースしよう!
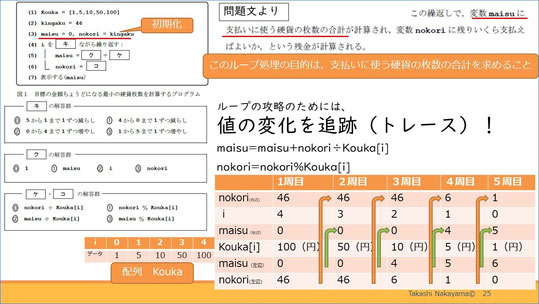
繰り返し文の問題攻略として一番大切なのは、値の変化を追跡、トレースする、ということです。
その上で、最初に確認するのは変数の役割です。ここでは、変数maisuに支払いに使う硬貨の枚数の合計、変数nokoriに残りいくら支払えばよいかについての値が格納されるということをまず確認します。変数maisuは0で初期化、2行目で46が代入された変数kingakuの値を、変数nokoriに代入しています。
※クリックすると拡大します
ここから、スライド右下の表を使って解説します。
まずiは4からスタートです。右辺の変数maisuは0、Kouka[i]はiが4なので、100です。46円支払うのに100円は使いませんので、左辺の変数maisuは変わりません。また、nokoriも変わりません。
次に2周目です。iは3になりますが、46円を払うのに50円は使いませんので、maisu、nokoriともに変化はありません。
3周目から変化がありますので、注意深くやりましょう。
iは2になります。右辺のmaisuは0です。そして、46円支払うのに10円は4枚使うので、左辺のmaisuが4になります。そして、nokoriは46を10で割った余りなので6です。
それが4周目に繰り越されます。nokoriが6、iが1となり、右辺のmaisuが繰り越されて4になります。6円の支払いにKouka[i]が1である5円は1枚使うため、4+1で左辺のmaisuは5、nokoriは1になります。
最後の5周目は、nokoriが1、iは0です。1円の支払いにKouka[i]はiが0である1円を1枚使うため、5+1で6となります。そしてnokoriは0になり、繰り返し終了となります。
このように、繰り返し文は前の処理が繰り越されます。その性質を踏まえて回答できるよう、復習していきましょう。
問3 問題の検討で迷ったら、コードの仕様を確認しよう
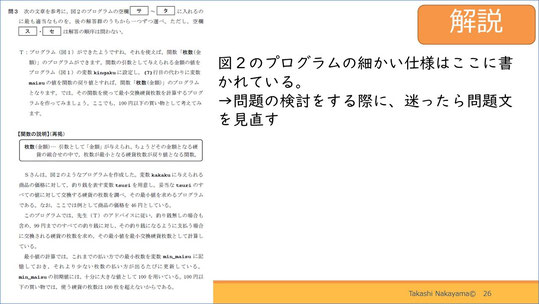
それでは、最後の問3です。
次のスライドに図2としてコードが書かれており、このプログラムの細かい仕様がわかります。ですから、問題の検討をしていて迷ったらここを見直すとよいでしょう。
※クリックすると拡大します
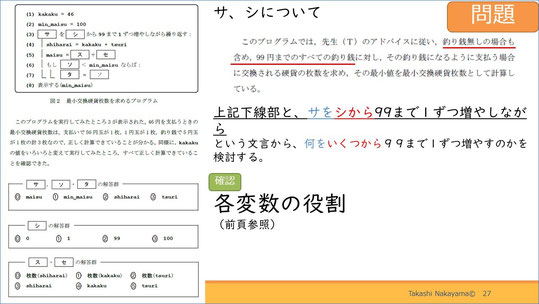
次に「サ」「シ」についてです。
これは右上の下線部を確認してください。「釣り銭なしの場合も含め、99円までのすべての釣り銭に対し」とあります。これを3行目の「サをシから99まで1ずつ増やしながら繰り返す」という文言を見て検討してみてください。
※クリックすると拡大します
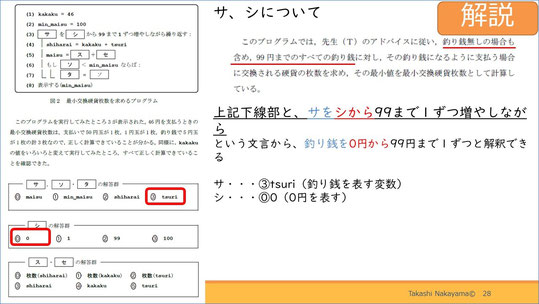
解説です。
これは、釣り銭を0円から99円まで1ずつと解釈できるため、「サ」は3のtsuri、「シ」は0の0が当てはまります。
※クリックすると拡大します
次は、「ス」「セ」です。
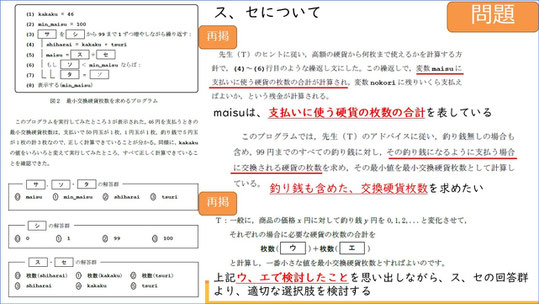
まず4行目、新たにshiharaiという変数があり、ここには価格と釣りの合計が格納されると書かれています。5行目のmaisu=「ス」+「セ」に当てはまる選択肢を答える問題です。
先ほどやったように思えて解答文を見てみると、割り算や枚数という選択肢がありません。
そこで、少し振り返ってみましょう。先の問いにあった通り、変数maisuは、支払いに使う硬貨の枚数の合計が入ります。そして、右側中ほどの下線部には「その釣り銭になるように支払う場合に交換される硬貨の枚数」とあります。ここで、求めたいのが「釣り銭も含めた交換硬貨枚数」であることがわかります。
そして、かなり戻りますが、問1の「ウ」「エ」で商品の価格をX、釣り銭をYとし、釣り銭を0、1、2と変化させて、それぞれの場合に必要な硬貨の枚数の合計を表した際に検討したことを思い出し、解答群の中から適切なものを選択しましょう。
※クリックすると拡大します
解説です。まず、右上の解説を見てください。
変数shiharaiは、商品価格と釣り銭が含まれているため、枚数(shiharai)+枚数(tsuri)が適切です。
この設問は、第3問の象徴的な問題で、最初に検討したことが最後に出ています。いわゆる伏線というものなので、近くの問題文を見てよくわからなかったりしたとしても、どこかにヒントがあるかもしれません。
※クリックすると拡大します
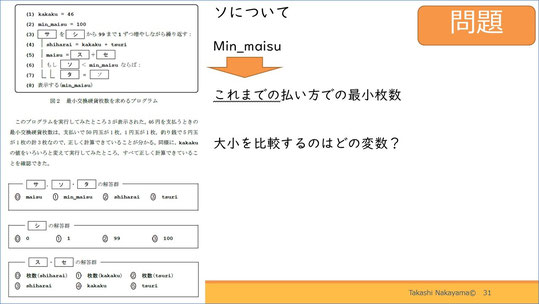
それでは「ソ」です。
6行目に、「もしソ<Min_maisu」とあります。Min_maisuとは、繰り返し文で求めてきた払い方のうちで、最小の枚数を格納する変数です。もし、「ソ<Min_maisu」ならば、6行目の条件を満たすと7行目の処理が行われます。
さて、Min_maisuと比較するのはどんな変数か考えてみましょう。
※クリックすると拡大します
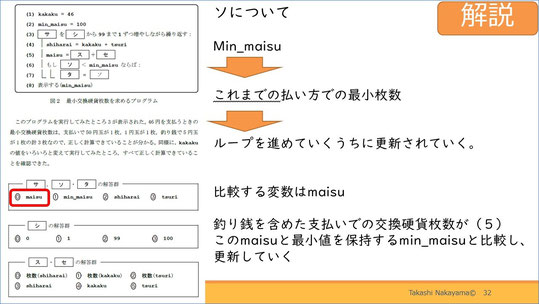
解説です。答えは0の「maisu」です。
Min_maisuとは、これまでの払い方の最小枚数です。繰り返し文を進めていくうちに、変数maisuがMin_maisuよりも小さければ最小値が更新され続けます。
※クリックすると拡大します
初期値のセオリーを覚えておこう
ここで、いろいろな初期値について見てみましょう。
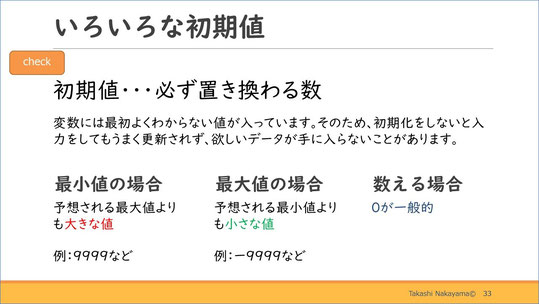
初期値は必ず置き換わる値を設定するのがセオリーです。今回のように最小値を格納する変数には、予想される最大値よりも大きな値を設定します。
今回の問題だと、100円以下の買い物で使う硬貨の枚数は100枚を超えないということで、Min_maisuには十分大きな値として100が格納されていました。
他にも最大値を格納する変数には、予想される最小値よりも小さな値を設定します。件数などを数える変数には、初期値として0を設定するのが一般的です。
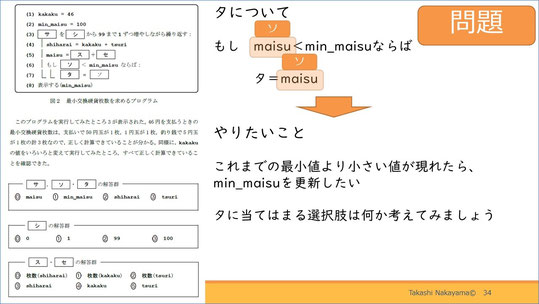
最後の設問「タ」にいきましょう。
先ほど述べた通り、これは変数maisuがMin_maisuよりも小さかった場合に実行する命令で、Min_maisuの更新をしますが、このためにはタに何を当てはめればよいでしょうか。
※クリックすると拡大します
解説です。
繰り返しになりますが、イコール(=)でつながれている命令は右辺のものを左辺に代入するという意味です。また、6行目の、もし「ソ」のmaisuがMin_maisuよりも小さかったら実行される命令で、最小値を更新したいということなので、ここは1のMin_maisuが当てはまります。
3行目から釣り銭を、0から99まで1ずつ増やしながら全ての硬貨交換枚数を調べ、最小値を更新していきました。ループが終わったらMin_maisuを表示し、最小交換枚数を表示するプログラムの完成です。
※クリックすると拡大します
情報オリンピックの予選問題に挑戦!
最後に、第3問、すなわちプログラミングの問題の対策についてお話しします。
今回、順次・分岐・繰り返しを混ぜた出題がありました。また、配列があり、短い文脈とコードからいろいろなことを考える問題が出題されました。このような問題の対策としては、情報オリンピックの1次予選の問題(※2)に取り組んでおくのがよいと思います。
※2 https://www.ioi-jp.org/problem_archive.php
また、もう少し敷居を下げた問題として、情報オリンピックのジュニア部門の「ビーバーチャレンジ」(※3)というものもあります。
※3 https://bebras-top.eplang.jp/

情報オリンピック自体は高校2年生までが出場対象ですが、3年生でもオープン参加可能ですし、過去問を見て学習することもできます。一次予選は4問出題されますが、その「問題4」を解ければ共通テスト対策は十分だと考えます。解説も載っていますので、挑戦してみてください。
神奈川県情報部会実践事例報告会2022オンライン オンデマンド発表より