オンラインイベント 教科『情報』授業のあり方を考える ～共通テスト試作問題をうけて～

試作問題の傾向から～グラフの読み取りや外れ値、回帰直線…難問・奇問ではないが、経験が必要

今回の講演依頼の話があった際に、先生方がデータ分析のところをどのように進めたらよいか困っていらっしゃるということをうかがったので、まずは11月の「試作問題」の「データの活用・分析」問題の解説から始めます。

今回の「試作問題」では、第4問の大問1個分が「データの活用・分析」に割り当てられており、そこだけで25点ということで、配点としては大きいと思います。

この配点が、本試験にそのまま引き継がれるかどうかとは分かりませんが、やはり大きな割合を占めると思って対策しておいたほうがよいのではないかと思います。

ここからは一つひとつ問題を見ていきます。

最初の第4問問1は、仮説を立ててデータを活用しようという問題です。いきなりデータ分析を始めるのではなく、最初に手元にあるデータでどんなことが考えられるかを考えて仮説を立てる問題で、こういうところは授業の中ではなかなか手が回りませんが、経験しておくことが大事であると思います。

よくある間違いとしては、「仮説になり得るかどうか」ということと、「そもそもの仮説が正しいか」ということを混同してしまう生徒がいるのではないかと思います。

学校でできる活動としては、例えば、「情報」や「総合的な探究の時間」で、きちんと仮説を立ててからそれを検証していく活動を経験して、仮説として成立しているのかどうかを考えさせることが大事であると思います。

※クリックすると拡大します。

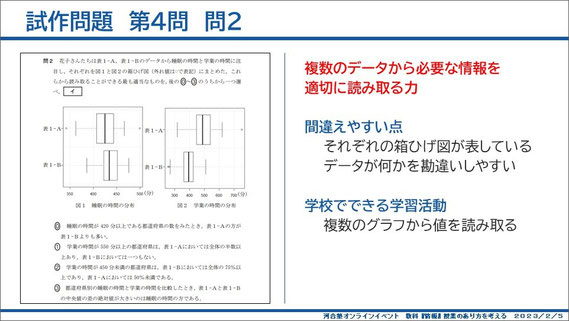
続いて、第4問問2は、箱ひげ図を読み取る問題です。図示されたものから必要な情報を適切に読み取る力が問われます。

スマートフォンの使用時間、学業の時間、睡眠の時間など様々な情報が組み合わされて図示されているので、それぞれが何を表しているデータなのか、勘違いしやすいのではないかと思います。

授業の中では、グラフなどを書くことによって、複数のグラフから適切に情報を読み取る経験をさせておかないといけないと思っています。

※クリックすると拡大します。

続いて第4問問3です。先ほどは、もともとのデータからすんなり書ける箱ひげ図でしたが、ここは、問題に「表1-Aから表1-Bとの値を引いた差」と書いてあるように、スマートフォンの使用時間が短い分と長い分の差を取るという、加工したデータから必要な情報を読み取る力が問われます。

そうすると、縦軸が何であって箱ひげ図が何を表しているのか、引き算をしているのが何から何を引いて、正負がどうなっているのか、といったところは読み違えやすいところです。限られた共通テストの時間内で、冷静に読み取っていく力が求められる問題です。学校の授業の中では、群を比較するために差や比を取ることは、なかなかやれていないところですが、このような比較の仕方があることを、この「試作問題」に教えられているように思います。。

また、今回は差を取りましたが、後ほど数学との棲み分けのところでもお話ししますが、実際に比較する際に、今回のように差が適しているようなデータもあれば、比率を考えた方が適しているデータもあります。ですから、差なのか比なのか、比べるときにはいろいろな考え方がある、というところを押さえておかなければいけないかな、と思っています。

※クリックすると拡大します。

続いて、第4問問4は散布図の問題です。散布図と箱ひげ図が同時に描かれているのは、なかなか見ない問題ですし、慣れていないと、どこに着目しなければいけないか、というところが難しく感じるかな、と思います。

また、縦軸・横軸で時間の刻み方が、若干違っているところも、気を付けなければいけないところで、これもグラフを読み取る力が問われることになってくると思います。

※クリックすると拡大します。

続いて第4問問5は外れ値の読み取りです。

外れ値は、四分位範囲を基に決めるという方法が使われることが多いと思いますが、ここでは標準偏差を使って外れ値を求めています。

数学の学習指導要領を読んでいくと、「外れ値の決め方は、四分位範囲で求める方法や標準偏差を使って求める方法がある」と書かれていますが、それが情報の「試作問題」に出てきたので、少しびっくりしました。

また、ここでは単回帰分析も絡んできています。単に回帰直線を引くところにとどめないで、きちんと推定値や残差を出して、予測値と推定値と実際のデータの差があるかというところを確認する経験がないと、この問題の理解は難しいかと思います。

※クリックすると拡大します。

「参考問題」では、移動平均や散布図行列、擬似相関を扱う問題も

今回の「試作問題」には、データ分析の「参考問題」も出ていましたので、こちらもざっと見ていきます。

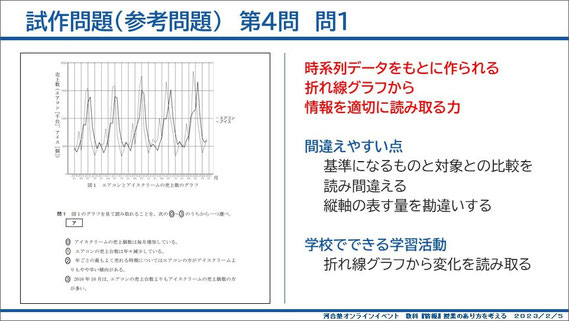
参考問題第4問問1は、折れ線グラフで時系列を追っていくというグラフの読み取りですが、縦軸の表す量もきちんと見ておかないと間違えてしまう可能性があります。グラフが表すものを正しく読み取る力が求められる問題だと思います。

※クリックすると拡大します。

続いて「参考問題」第4問問2は、時系列データにおいて、移動平均を使って平準化を図るという問題です。

周期性を打ち消して全体的な傾向を見るためにはどうしたらよいか、ということは、初めて見ると分かりにくいかもしれません。

ただ、移動平均の概念を説明する際に、最近の話題でいえば、新型コロナの新規感染者数で週7日間の平均を取っているというのは、曜日の影響を打ち消すため、というのは説明として使いやすいかなと思います。

※クリックすると拡大します。

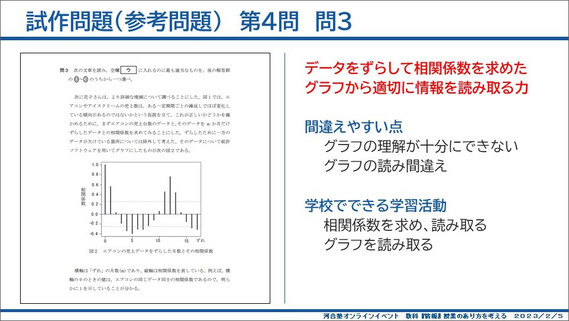
第4問問3は、時系列データで時間をずらして、自分自身のデータとの相関係数を取って、その相関係数の値をグラフにしたという問題です。相関は相関でも、自分自身のデータと相関を取るというのは、これもなかなかやっていないことかもしれません。

これも問題を解く上では、単にグラフの読み取りということになりますが、どのような操作をしているかを理解できることも必要かなという感じです。

※クリックすると拡大します。

続いて、「参考問題」第4問問4も時間軸をずらすのですが、エアコンとアイスクリームの売り上げの2つをずらしています。表の数値が意味するものを読み取っていないと、2つをずらしたときに、どちらを先行させるのか、どちらが後ろになるのか、というところで混乱しそうです。これもテストで初めて見ると難しく感じるだろうなと思いました。

※クリックすると拡大します。

続いて「参考問題」第4問問5です。これは、2021年3月の「サンプル問題」で、サッカーのワールドカップの問題を題材にした問題で「散布図行列」が出ていました。今回も、散布図行列や相関行列が出てきています。

こういった散布図がたくさん並んだところからの読み取りは、初見だと生徒はびっくりすると思いますが、基本的には、散布図や相関係数の読み取りになっているので、相関係数や散布図が表すものを理解しておくというところが必要かなと思います。

また、擬似疑似相関や交絡因子といったところも出題されています。ここでは、エアコンとアイスクリームの売り上げの関係を考えていますが、ここには気温が関係してるだろう、という常識的な答えになっていますので、ある程度常識ということも大事になってくるかと思います。

※クリックすると拡大します。

※クリックすると拡大します。

条件を設定するため、問題文はどうしても長くなる。問題文の読み方の「強弱」に慣れておく必要も

「試作問題」をご覧になって、文章量がかなり多いと感じられた先生が多いかと思います。この辺りは、他の先生方とかなり重なりますが、今回の「情報」の学習指導要領には、「情報活用能力とは、世の中のさまざまな事象を、情報とその結びつきとして把握し…」といったことが書かれています。

様々な事象と結びつけるということになると、一個一個について具体的な状況の設定の説明が必要なので、問題文が長くなってくるのは仕方がないかなと思っています。

ただ、問題解決の流れに慣れて、じっくり読むところと、そうでなくて軽く流すところの重みづけには慣れておかないと、なかなか読み切れないかなと思っています。

統計手法の知識で対策しようとするのは得策ではない

今回の試作問題で使われていた統計の考え方をまとめたのが、下のスライドです。作問された先生は本当に様々な統計的な背景を持って作られていてすごいな、と思いますが、一方で出題されたからといって、こういった個々の知識にはまり込んでいくのは、高校の「情報」の授業としては得策ではないと思います。

授業では、グラフの読み取りや、相関係数や単回帰分析など、高校で求められている基本的な概念を定着して、それを基に思考・判断・表現できるようにしていくというのが重要だと思いますので、こういった手法的な部分の対策はやらない方がよいと思っています。

数学の試作問題との比較～「情報」は問題解決の視点でデータを捉え、データの読み取りや解釈をしていく

「データ分析」の部分については、数学との兼ね合いも大事になってきますので、そのお話をしていきます。

数学ではやはり計算が多いかなと思います。四分位数の求め方や、箱ひげ図を作るのに散布図上の点の傾きを使っているところが数学っぽいなと思いました。

あとは、データを加えた際に数値がどのように変化するか、というところで、標準偏差や相関係数の変化を数学的な視点で見ているなと思いました。

※クリックすると拡大します。 

※クリックすると拡大します。 

※クリックすると拡大します。 

※クリックすると拡大します。

仮説検定については、数学Aで確率を学び、数学Ⅰで仮説検定が出てきます。そのため、仮説検定では確率が使えないので、コインを投げたときの相対度数を基に仮説検定をしているということが、数学の先生とお話ししていて分かりました。

それでは「情報I」ではどう扱われているか、というと、学習指導要領ではなく「学習指導要領解説」の方に、「データの傾向について評価するために、仮説検定の考え方を扱ったりすることも考えられる」ということで、弱めに書かれています。仮説検定が「情報」で実際どう扱われていくのか、ということは、今後の出題傾向を見守っていく必要があると思います。

私見としては、数学と「情報」の兼ね合いは、「情報」は問題解決の視点でデータを捉えること、そこでデータの読み取りや解釈をしていくというところがポイントであると思います。一方数学の方は、値の求め方や統計量の数学的な性質がポイントとなっているのではないかと思います。

また、「なぜ『情報』で統計やデータを扱うのか」とい疑問を持たれる先生いらっしゃるかと思います。

これについては、ビッグデータの処理やAIの進展ということを考えていく上では、「情報」でその仕組みを体系的に学んでおくことが必要であると思います。

特に、機械学習の「予測」のところで、単回帰分析は最初の入り口になりますので、「情報」でこういったデータの活用を学んでおく必要があるのだと思います。

さらに先を見据えるために

今回の「試作問題」だけではなく、大学入試センターのサイトをいろいろ見てみました。

11月に、今回の「試作問題」が公開されたのとほぼ同じ時期に、「CBTの調査研究について」(※2)という報告書が出ています。

※2 大学入試センターにおける CBT（Computer-Based Testing) に関する調査研究について

※クリックすると拡大します。

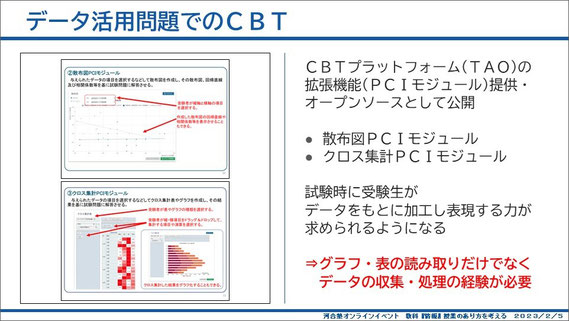
CBTプラットフォームのモジュールで見ていくと、散布図を書くモジュールやクロス集計をするモジュールといったものがあるようです。これらを使うと、データの読み取りだけでなく、実際にデータを収集して処理して、グラフや表にしていく、という出題も可能なので、こういったことも経験しておく必要があるのかなと思います。

※クリックすると拡大します。

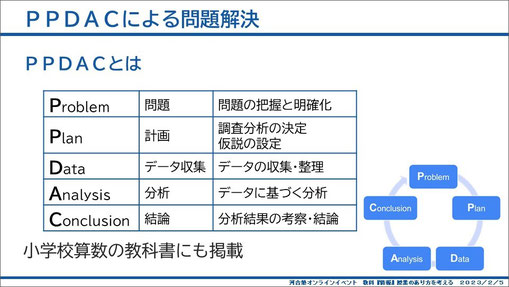
データ分析の授業～PPDACサイクルを踏まえることが重要

実際の授業でどのようなことをしたか、ということをお話ししていきたいと思います。

データを使った問題解決ということで、問題→計画→データ収集→分析→結論というPPDACサイクルで考えていくことが重要になります。これは小学校の教科書にも載ってます。

※クリックすると拡大します。

■質的データの分析～関係がありそうな2つの事象にいてアンケート調査でデータを収集し、クロス集計とカイ二乗検定で検証する 

ここでご紹介するのは、まだ「情報I」のデータ分析がどうなるか見えなかった時期にやってみた、質的データと量的データの分析の実践です。

まず「質的データの分析」では、生徒に何かしら関係がありそうな2つの事象を考えて、アンケート調査でデータを収集し、クロス集計して、カイ2乗検定で検証する、ということを行いました(※)。

※ 生徒が協働的に学ぶデータを活用する授業の成果と課題

私の方から、答えが見えている問題を与えてやらせても、結局合っているかどうかのチェックだけになってしまって面白くないので、生徒自身に問題を考えさせて、自分たちで検証するという流れで行いました。

授業では、4人程度のグループで、関係しそうな2つの事象を考えました。あるグループは、スポーツをすることが好きなことと、スポーツを見るのが好きなことは関係があるかを確かめてみたい、と考えました。

実際にどういった選択肢で質問しようかという検討をしながらアンケートを設計し、実施しました。写真では対面で行っていますが、もちろんGoogleフォームでもできます。

ただ、限られた授業時間でフォームを作って、全グループのフォームを網羅して…というのはなかなか難しいので、対面であることを生かして、紙を使ってアンケートを実施しています。

こちらは生徒が行った分析です。クロス集計では、「スポーツを見る/スポーツをするのが好き」を〇、「嫌い」を×として図にします。

これをカイ2乗検定するのですが、計算式をExcelで入力して、Excelの関数で求めた棄却限界 と比較をして、その結果によって差があるかどうか、ということを考えます。このグループは、スポーツをするのが好きか嫌いかで、見ることが好きか嫌いかの差があるとはいえない、という結論に至りました。

こういったことを、グループごとにいろいろな問題を発見し、アンケートを作って検証した、という授業です。

■量的データの分析～基本統計量を求めて、散布図を描き、t検定で相関の有無を検証する

量的データの分析では、いろいろな基本統計量を求めて、その後相関係数を出してみることで、本当に相関があるのかどうか、無相関検定というのを試しにやってみたというものです。

一つひとつの統計的な背景までは分かっていないところはありますが、仮説検定の流れを経験してみるための授業を設計しました。

こちらもあるグループの例で説明します。

 彼らは、「手が大きいほうが、スマートフォンで文字を入力するスピードが速いのではないか」という仮説を立てたグループがあります。本当にそれが成り立つのかどうか検証してみようということをやってみました。

分析の計画で、生徒たちは「スマートフォンの文字の入力が速いかどうかには、ふだんからスマートフォンを使っているので入力の癖があるのではないか」といったことに気付きました。そこで、ふだん絶対に入力しないような文章を入力してもらうことにしよう、という計画を立てて、入力してもらう文章を「崖の上のポニョが横断歩道で側転」として、これを入力する速度を測りました。

このスライドの写真は、手の大きさを測っているところです。このような実測をしてデータを集めました。そして、基本統計量を求めて、散布図を描画したり、t検定によって相関の有無を検証したりしました。

この辺のやり方については、「こういった計算をすると求められるので、その通りやってみなさい」と指示して行いました。

結果としては、まず統計量から、手の大きさの分散は小さいけれど、入力速度の分散は大きいということを見つけることができました。また、手の大きさと入力速度の相関については、相関があるとはいえないということになりましたが、生徒たちからは、「(入力速度は)スマートフォンの利用時間と関係があるのではないか」という、次の課題が見つかりました。

この検証までは時間的には無理でしたが、PPDACのサイクルの次のサイクルにつながる問題が見つかったというのは、このグループの成果かな、と思っています。

問題解決の文脈でデータを活用する授業を大切に

授業を行った効果と反省点です。

効果としては、問題の設定から結論を求めるまでの一連の流れを経験できたというのは大きいと思います。また、自分たちが決めた問題に取り組んでいるということから、生徒の視点での問題意識を発揮することができ、主体的に取り組んでいたと思います。

ただ、4人で1グループとした関係で、個々のグループの問題設定が適切であるかどうか、また結論が妥当であるかどうかというところまでは、なかなか難しいところがありました。また、これ以上の複雑な分析は、なかなか難しいと思います。

最後にまとめです。大学入学共通テストは、資料から読み取る問題は多そうですが、高校の範囲を超えた知識を用いるものではないので、一つひとつのデータの活用の授業をきちんとやっていく必要があると思います。また、将来に向けてCBTの可能性もありますので、データの読み取りばかりで終わりにしない方がよいかと思っています。

高校での入試対策は、問題解決の文脈でデータを活用する経験をさせることともに、「情報I」を1年生で行うので、入試に向けた教材や補講などがあるとよいと思います。

【質疑応答】

Q1.高校　情報科・技術科教員

サンプルデータは、実際に生徒に調査させる以外、どのようなデータをお使いになっていますか。大量のデータを取得するにはどうすべきか、悩んでいます。

A1.春日井先生 

 今年の授業では時間配分をミスしてしまい、データの活用を指導できる時間が少なくなってしまいましたので、限られた時間で時系列データ、単回帰分析、擬似相関と交絡因子について生徒が理解できるようなデータを探しました。

そこで、熱中症の疑いでの搬送人数、電力使用量と最高気温のデータを用いて授業を行いました。最高気温を説明変数、熱中症の疑いでの搬送人数を目的変数として単回帰分析をしたところ、梅雨の晴れ間の日に熱中症の疑いでの搬送人数が大幅に上振れしている興味深い結果が出て、データをもとに考えるきっかけになりました。

授業での目的にあわせて、データの量を確保するのがよいか、外れ値を含むデータがよいか、ある程度相関がみられるデータがよいかといった観点から探しています。

Q2.高校　情報科教員

四分位数の計算では、少ないデータで計算する場合、高校数学での計算結果と、エクセル関数での計算結果では（四分位数の定義の違いのため）、若干の違いが生じるということも、この情報科の教材研究をする中で初めて知りました。今使用している教科書と副教材では、問題の正解が高校数学の値と異なるような問題があり、指導法で非常に悩んでいました。どのように指導すべきか、お考えをお教えください。

A2.春日井先生

 数学Ⅰ・Ａの試作問題で四分位数を求める問題が出ていました。生徒の混乱を避ける観点で、あえて計算方法に踏み込まない方がよいと思っています。

その一方、数学での求め方で求めた値とコンピュータを利用して求めた値が異なることに直面することにもなり、まったく触れないで済ませることもできません。

詳しくは三重大学の奥村晴彦先生のWebページ(※3)をご覧いただきたいのですが、四分位数を求める考え方やプロセスが複数あるので、値が一意に定まらないことはむしろ自然なことだと思います。

データを用いる際には、数値そのものが重要なのか、データから読み取れることに意味付けすることが重要なのか、判断して決めることになると思います。

四分位数について付け加えると、計算では「包括的な中央値」により求めるQUARTILE.INC関数で求めているにも関わらず、箱ひげ図ではデフォルトになっている「排他的な中央値」QUARTILE.EXCで求めた値で描画されていて、値が一致しない図表をときどき見かけることがあります。

そのような図表に気が付いたときには、やはり違和感を感じるので、そろえる必要があると思います。

  ※3 三重大学奥村先生のWebページ　

Q3. 高校　情報科教員

座学はどのような形で、どの程度時間をかけてしていらっしゃいますか。もし座学をしないのならば、知識等の習得はどのような形で生徒にさせていますか。

A3.春日井先生

 ちょうど座学の在り方について見直しているところで、その過渡期に考えていることを回答いたします。

教科書等に書かれている知識を一斉に伝達するのは、教室に生徒がそろう授業時間の使い方としてもったいなく思えてきました。そうとはいえ、教科書の紙面だけで理解できる生徒ばかりではなく、説明を耳から聞くことで理解できる生徒や、手順を追って一つ一つ説明されることで理解できる生徒もいるので、動画（というより音声付きスライド）を撮影して視聴できるようにし始めたところです。

動画は内容を細かく区切って、１テーマ３分程度（長くても５分以内）になるように試みています。動画を作ったからといって反転授業にしようとは考えていません。授業内で要点を確認したり、学習活動と組み合わせて知識を確認できるようにしたりできそうに思っています。

Q4. 高校　情報科教員

このような授業をなさったときの評価方法を教えてください。

A4.春日井先生

 はじめに「評価」が指しているものを整理しておきたいと思います。成績を付ける「評定」と学習状況を測る「評価」とがあると思いますが、後者について主に説明していきます。

「評価」は、学習活動が適切に行われているかを測る、学習活動中の評価であるいわゆる形成的評価と、学習の最後に行う総括的評価とに整理できます。

学習の途中段階では、多くのグループに分かれて活動しているので、記録して成績を付けるために使うような評価は、現実的には難しいと思います。それよりは、生徒の学習活動の状況を測り、確実に学習を進められるように支援していく必要があります。

そのために、グループの進捗状況を生徒に説明させて、それに対してコメントを述べることで行っております。よく「指導と評価の一体化」といわれていますが、適切な指導をするためには評価が必要で、評価を伝えることは、指導にもなっていると思います。

形成的評価、および総括的評価としてルーブリックを用いた自己評価もさせました。ルーブリックで、評価の観点と基準を示すことも指導になります。

また、生徒に学習活動を振り返って、グループ活動の一連の学習活動を文章でまとめさせました。学習に主体的に取り組んだ生徒は文章を詳細に書けますが、そうでない生徒にとっては文章が薄くなる傾向があります。

いずれにしても、評価を行うためには、生徒の活動が表出する機会を設けたり、生徒が内省する機会を設けたりする必要があり、これらを組み合わせて多面的に評価しています。

評定を付ける際には、総括的評価と成果物の評価を使っています。

オンラインイベント「 教科『情報』授業のあり方を考える ～共通テスト試作問題をうけて～」講演より