事例281

基数変換の計算問題は、「情報I」の内容では珍しく、ドリル的な問題練習が可能なので、練習すればテクニックを身に付けることは可能です。

しかし、基数変換は、旧課程の学習指導要領では、「コンピュータと情報通信ネットワーク」の単元で扱われていました。基数変換、特に2進法はコンピュータの動作やネットワークのプロトコルの基礎であり、「情報I」で言えば「コンピュータとプログラミング」「情報通信ネットワークとデータの活用」と密接につながります。2進法の「01」が、コンピュータの動作やネットワークのプロトコルにどのようにつながるかを生徒に気づかせることが、非常に重要なのです。

今回は、東京都立南多摩中等教育学校の御家雄一先生の「基数変換(少し画像)」の授業を見学しました。

ピクトグラムの人型でON-OFF⇔0-1をつなぐ

御家先生の「情報I」の授業で通年使用するキャラクターが「人型ピクトグラム」。授業内では省略形で「ピク」や「ピクさん」と呼ぶことが多いです。御家先生はピクトグラムの特性に着目して授業に活用しています。特に人型に着目しています。人型のピクトグラムは「情報デザイン」やプログラミング、データ分析を統合して学ぶ仕組み「ピクトグラミング」でも使用されています。

授業では、木製の人型ピクトグラムを生徒が手元で実際に動かしながら考えます。どの単元も同じキャラクターを使うことで、唐突感なく単元同士のつながりを意識することができます。 

なぜアナログ→デジタルの変換が必要か

今回の授業のテーマは「基数変換」。基数変換というと、10進数を2進数で表すために、商が1になるまで2で割り続け、商と余りを下から読み上げていく演算(すだれ算)がまず浮かびますが、この授業では「なぜアナログ→デジタルの変換をするのか」という意味を理解するところから入ります。

御家先生の説明を聞いてみましょう。

アルコール温度計の目盛りを読み取る際に、アルコール柱の先端が目盛り同士の中間の位置に位置することがあります。「この柱の高さはどの程度か」ということは連続的に無限に細かく見ることができます(＝アナログ)。これを区切って読み、数値で表現した瞬間、デジタルに置き換えられたことになります。

デジタル温度計であれば、最初から「24.4℃」「24.5℃」のように数値で表現されますが、24.4℃と24.5℃の間の量が消えたわけではありません。この場合は、最初から0.1℃刻みの別の物理量に変換したものが表現されているわけです。

ピクの表裏で物事を表すことを考えます。23℃と24℃を表すには、黒であれば23℃、白であれば24℃、ということにすれば、1ピク(人型ピクトグラム1体)で表すことができます。このように目盛りのそれぞれにピクを配置して、表-裏でON-OFFを表現します。この担当するピクを増やすことで、より細かい値を表すことができます。

このピクは、コンピュータの中の回路で電気が流れる-流れない、電圧が高い-低いに置き換えることができます。

このピクの表・裏を、電球の点滅に置き換えてみます。白の面は電球が点いている、黒の面は電球が消えている、と表すことができます。さらに、磁石のN極・S極のどちらが上になるかで表すこともできます。

このままでは見にくいので、OFFを0、ONを1に置き換えたのが、一番右の2進法の表記ということになります。

「情報」で非常に重要なのは、温度計の数値などの表し方で、ピクの表-裏と01のパターンとのつながりがしっかり理解できていることです。数学のように2進法の計算ができるようになることがメインではありません。

ただ、2進法の計算ができなくてもよいということではありません。「情報」でやっていることは2進法の応用なので、計算もできるようになってくださいということです。

画像のデジタル化と復号を通して2進法→16進法を体験する

ここからが今回の授業のメインの活動です。

前回までの授業で、10進法の数を2進法、16進法で表現する方法は学んでいます。

※クリックすると拡大します

さらに、2進法の4桁は16進法の1桁に対応します。表記のパターンはこの表のとおりです。

※クリックすると拡大します 

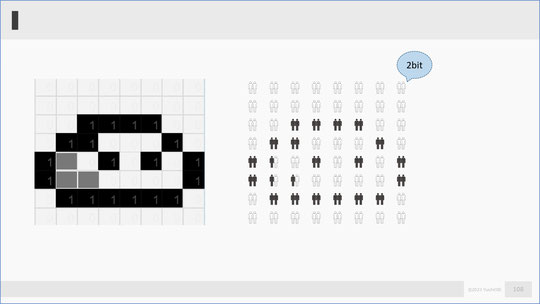
左の絵は、8×8マスのマス目に色を塗る-塗らないで描かれています。このマス目の表裏をピクに置き換えて、ピクの白い側を白のマス、ピクの黒い側を黒のマスとしたのがスライドの右図です。

この絵の頬のところに別の色を入れてテレているようにしたい。そのために薄く色を入れたい、という場合、ピクが1マスに1つのままだと黒か白のみの表現になるため頬が黒の塗りつぶしになってしまいます。

そこで、ピクの数を増やして、1マスに2体ずつ配置する、つまり1マスを2bitにすることで、「白白」「黒白」「白黒」「黒黒」の4パターンになります。「白白」は白、「黒黒」は黒。新たにグレーを「黒白」に設定すると、イラストに半分の濃さの色を付けるということができます。このように、ピクのパターンとマッチさせるということが重要なのです。

ここからが生徒の作業になります。実習の目標は、自分で描いた絵をデジタル化して他の人に伝える。そして、他の人のデジタル化された情報を復元するということです。

手順がこちらです。

1. 8×8のマス目(1)に、罫線にとらわれず太い線で自由に絵を描く。

2.(1)の半分以上に塗られているマスを1、塗られていないマスを0としてマス目(2)に転記する。

　→デジタル化(量子化)

3.(2)で書いた数を2進数と見なし、16進数に変換して(3)に記入する

　→2進法から16進法への基数変換

2.で重要なのは、自分が描いた絵(＝アナログ)を2進法に置き換えて表記しますが、これがON-OFFのビットパターンであることを意識することです。

3.では、2進法で書かれた数字を16進法に変換します。これは、「01の羅列は桁数が多くて読みにくいので、人間の都合でおおよそのデータ量を把握して受け取り易くするために16進法に置き換える」という意味があることも説明します。それを実感しやすいように、右側に二進法と十六進法の対応表を表示しています。これは変換の作業を練習することが目標ではなく、利便性を実感することが目的のためです。

このように、デジタル化や基数変換などの作業の意味、使われる場面などをその都度きちんと押さえながら進めます。

※クリックすると拡大します 

16進法に置き換えたデータを、アンケートフォームに提出します。提出された十六進法の羅列は生徒に公開します。

生徒は、自分のデータを提出できたら、他の人の作品を自分のワークシートに転記して復元します。

※クリックすると拡大します 

※クリックすると拡大します。

生徒がある程度復元できたら、十六進法の羅列から二値画像に自動変換した内容を先生が公開します。生徒は自動で二値画像に変換したデータと自分で復号したデータを照合します。この作業を通して、2進法と16進法は親和性が高いことが体感できます。さらに、データ上は正しく復元できても、デジタル化することで、もとの絵の微妙なニュアンスが失われることもわかります。

2進法は「ニコイチ」で考える

作品の復元の実習が終わったところで、先生がピクを使った基数変換の概念を詳しく説明します。生徒は手元のピクを操作しながら説明を聞きます。

基数変換は、量的には同じ数を、「2」「10」「16」などをベース(＝基数)として、使う分野や目的によって表し方を変えるということです。たとえばふだんの生活では10進法、コンピュータでは2進法、2進法を人間が見やすくするためには16進法を使います。

御家先生は、2進法の説明に下の写真のような「ゲート」を使っています。ゲートは裏が0で、表が右から1,2,4,8,16の桁を示します。

各ゲートには、表に示された数(＝人数)の組単位のピクしか入ることができません。そのためには、2人1組のペア(＝「ニコイチ」※)を作っていくことになります。

　※「いつも一緒の2人」という状態を表す、(現在は死語?の)若者言葉。流行初期は2娘1(読みはニコイチ)という表記であったが、現代ではニコイチというカタカナ表記も見られる。

たとえば、例えば3人であれば、「2」のゲートに2人の組と「1」のゲートに1人が入ることができます(→2進法表記の11)。

4人であれば、2人の組が2つできるので、中央の「4」のゲートにそのまま入ることができ、「2」「1」のゲートには入らないので0となります(→2進法表記の100)。

これをピクが5人の場合、6人の場合、7人の場合…と考えていきます。ポイントは「ニコイチ」をどんどん作って、余ったピクから小さい桁のゲートに入れていくことです。

これを割り算で考えます。6人のピクがいる場合、6÷2＝3というのは「6人を2組に分けると3人ずつに分かれる」と、「6人を2人ずつ(＝ニコイチ)に分けると3組できる」という2つの見方ができます。ここでは後者を使います。

今度は7人を2人ずつに分けると

7÷2＝3…1

「ニコイチ」が3組できて1人余ります。余ったピクは「1」のゲートに入ります。

さらにできたペア3組の中で「ニコイチ」を作ると、

3÷2＝1…1

となります。

このように、ペア同士が2組くっついたものが1組、2人1組が1組できます。この2人1組は「2」のゲートに入り、ペア同士2組は4人いるので「4」のゲートに入ることかできます。

この商と余りを矢印の方向に読み上げると2進法の表記になり、さらに続けて2で割っていく計算の表記はスライド右のようになる、というよくある「すだれ算」の説明になります。

「なぜ基数変換を行うか」を常に意識させる

一連の説明の中で、先生が繰り返されていたのは2進法に変換する算術の方法ではなく、「なぜこのような表記の変換を行うか」「なぜこのような計算方法(すだれ算)になるのか」ということです。

「ゲートに入る」「ゲートに入らない」は、「情報」で言えば電気回路のスイッチのONとOFF、あるいは磁石のN極とS極を示します。

これを1と0で表すと数学の領域になりますが、重要なのは1-0がON-OFFとつながることです。コンピュータの動作を司る論理回路や真理値表は、全てここでの理解がベースになります。基数変換は、ともすれば答えを出しやすい表記の変換や計算に比重が置かれがちですが、木の人型ピクトグラムという実物を、ピクという愛称で呼んで親近感を持ちながら操作しつつ、わかり易い説明を聞くことで、この重要なポイントが意識できるようになっています。

※御家先生のこの授業の授業動画は、こちらをご覧ください。

授業の中にちりばめられた様々な工夫

作業や説明だけでなく、授業の中には理解を深めたり、「情報」への関心を高めたりする様々な工夫を見ることができました。

■「身の回りにある情報技術」に目を向けるきっかけを作る

授業の本題に入る前に、御家先生が先週出張先で撮られた写真が紹介されました。軽やかなトークの中で、街角やイベント会場内で見かけられた信号やピクトグラムの写真から、「情報」の授業で学んだものが身近なところにあることや、それが何を意味するかについて触れられ、「身の回りにある情報技術」を意識することを促す内容となっていました。

■「デジタル」を運指で表現

授業や動画の中で先生が繰り返して見せておられたのが、片手の指を曲げたり伸ばしたりして0から31までの数字を表現する方法です(生徒の中には、すでにスムーズに運指ができるようになっている人もいました)。前の授業で、先生は「デジタル」の語源はラテン語で指を意味する「digitus」であることを説明されているので、指の動きと連動させることは、デジタル表現のイメージと1-0の表記がつながって、理解を深めることになります。

■書画カメラの活用

今回のイラストの復号の作業では、イラストから2進法表記→16進法表記に変換していく手順をきちんと押さえる必要があります。ここでは、先生が説明しながら、生徒と同じワークシートで作業を進める様子を書画カメラで撮影し、生徒の提示用モニターに表示します。

考え方のポイントや注意すべき点などもここで示されることで、作業を進めながら同時に重要な点をつかむことができます。

御家先生に聞きました

今回の授業のポイントと工夫された点を教えてください。

今回の授業の最大のポイントは、基数変換を数字ではなく、パターンマッチングとしてとらえることです。ある情報をON-OFFで表現することと、コンピュータの中で電気が流れる・流れない(＝CPUの仕組み)が概念としてつながることが重要なのです。

中学校受験で記数法が出題されることがあるので、裏技的な変換の仕方を知っている生徒もいますが、そういう人も計算の意味が解っていません。ですので、ここでは「意味」の部分に重点を置きました。

前回までの授業で、アナログとデジタルやn進法について学んできているので、今回は、2進法⇔16進法の基数変換とデジタル画像の復号を経験する、という流れでした。

もともとこのイラストの復号の活動は、立川高校の佐藤義弘先生の「カラーの画像を16進法で表したものを復号する」というものをアレンジしたものです。一度に複数の色まで扱うのは大変なので、この段階でまずシンプルな線描で符号化まで扱ってしまうことで、それぞれの記数法の用途や、「情報」と数学の境界についても触れられるようにしました。

「情報I」全体としての授業の展開では、どのようなことに留意されていますか。

共通テストに「情報I」が入ったことで、ゴールを高3に置くか、いったん1年生で完結するかということは考える必要があると思います。

授業で心がけているのは、なるべくコンピュータサイエンスの一部を体験できるような実体験をさせることです。スタートでは難しいことは扱わず、いろいろ手を動かしたことのゴールが教科書になるようにしています。

言い換えれば、教科書は自習用の教材で、授業でやったことは教科書にはこう書いてあるね、という確認のために使うという感じです。

問題演習は、現在出ている教科書会社が出版している問題集を使い、期末考査の出題は情報入試の過去問や大学入試センターの試作問題などをアレンジして使って、なるべくその場で考える経験ができるようにしています。

取材を終えて

「情報I」の単元の内容を見ると、「情報デザイン」「コンピュータとプログラミング」「情報通信ネットワーク」のそれぞれに出て来る「01」が何を意味するのか、どのようにつながるのかを理解することが非常に重要であることを感じます。

今回の御家先生の授業では、テンポよいお話の中に「デジタル」の意味や働きが繰り返し説明され、「情報」と数学での2進数の扱い方の違いを印象付けていました。このステップを踏んでおくことで、論理回路や通信プロトコルなどに「01」が登場したとき、その意味するところをコンピュータの動作とともにイメージすることができることがわかりました。

今回の授業の中では直接出て来ませんでしたが、御家先生の授業では用語の意味を説明する中で、「digital←指」のように語源を示すことを重視していらっしゃいます。例えば、媒体・媒介物を意味する「メディア」は、中庸・中間を意味する「ミディアム(medium)」の複数形であることを、ステーキの焼き加減を表す「ミディアム」を例に引いて説明されています。語源を知ることで、「メディア」の意味を、そのニュアンスも含めて理解することにつながります。

「情報」は習得しなければならない用語が多いことが負担感につながりがちですが、字面だけでなくその意味とともに理解することが、より深い理解につながることを感じました。