事例286

学校はあと数年で100年を迎えます。１学年5クラスで200人ですので，6学年で1200人程度の小規模校です。私の紹介も少しだけさせていただきますと，いろいろな学会等でお役をいただきながら，昨年度は日本産業技術教育学会では学会賞を，ICT夢コンテストでは優良賞をいただきまして，それらを励みにしながら実践活動に邁進しています。

日常生活の一場面を想起できるように論理回路を説明する

それでは本題の，論理回路に関する授業の紹介です。今までこの単元は，どう教えたらいいか，悩みの種だったのですが，2022年11月公開の大学入学共通テストの「試作問題」(※)を見て光が差しました。

※2022年11月公開の大学入学共通テストの「試作問題」

本校が使用している教科書では，論理回路は「コンピュータのプログラミング」2頁程度の取り扱いだったと思います。生徒に対する知識のつかみ方のレクチャーでは，このスライドのようなアプローチになっています。コンピュータは「演算で全ての処理を行う機械」であり，「複数の論理回路の組み合わせが中枢となって構成」されており，その回路を幾つかまとめたものを集積回路といいます。そして，論理演算の仕組みでは，基本論理の3つの回路，つまりAND回路，NOT回路，OR回路を紹介しています。

授業のイメージとしては，最初に教科書の内容は伝えますが，それに加えて，例えばマザーボードを見せて「コンピュータの中はこうなっているんだよ」という話もします。また，それらがたくさんの半導体でできているという，素子の話もします。

この話をすることで，日常の出来事と生徒との接点を作ることができますので，ここは大事なキーワードとして仕掛けています。

次に例題に取り組むという形で，早速「試作問題」に挑戦してもらい，その後でさらに自分たちとの接点を考えるという活動をしました。

ここでは，特に生活の一場面を想起させるような基本論理回路について伝えるようにしているところがポイントです。つまり，ここでは，NAND回路やNOR回路などには深入りせず，演算の仕組みについて，「このような回路で信号が来ると，このように処理されて，出力はこうなる」ということを図示するようにしています。

基本的には，私はいわゆる入試問題はなるべく解かせないようにしていますが，この試作問題については，すごく光が差すようなものだったので，やらせてみたいな，ということであえてやってみました。

3つの基本論理回路の構造を身近な事例から説明する

AND回路については，「両方条件がそろったときにうまくいくこと」である，という話をします。

例えば車のライトを点けるには，車のエンジンが掛かっていないといけなくて，かつ，ライトのボタンがオンになっていないといけない。そんなイメージです。

NOT回路については，「出たものとは違うもの，真逆のものになることだよ。だから，消えたものが点いて，点いたものが消える。これはセンサーが反応して，電気が点いたり消えたりするイメージです。

OR回路は，「どれか一つが1(オン)になるものを考えてみたら幾つかあるんじゃないの？」という話をして，この3つの回路が基本となっていろんなことができるようになる，その最たる例がハーフアダー（半加算器）であるという話を最初の山場とします。

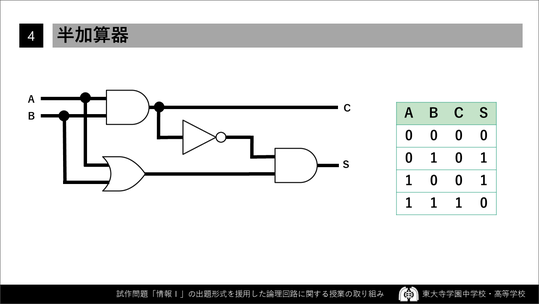
ここからが半加算器の説明です。「この半加算器というのは，この3種類のものだけで，あの演算ができるんだ。すごいよな」といった話を，私自身の感動をこめて語ります。

生徒は皆，目でAとBを追って，真理値表の該当する所を見て「うんうん」と納得します。

そしてしばらくすると「おおーっ」という顔付きになっていきます。

それからS（Sum）と桁上がりのC（Carry）の話をして，「このたった3つの組み合わせだけで，2進法の計算ができるようになるって，すごくないか？　しかも，こんなシンプルに。これ考えた人は絶対すごいよな！」という話をすると，考えるのが好きな生徒は，表情を変えて関心を持つようになります。

そして，「桁上がりにも対応しているものは？」ということで，半加算器が2つとOR回路だけで，桁上がりにも対応していけるような計算ができるんだよ，と全加算器の話をして，この3つの回路だけで全ての演算ができるようになっていることを示します。

スライドを活用して，２進法加算の繰り上がりイメージを想起

ただ，得手不得手もあり，一瞬で理解できる生徒ばかりでもないので，もう少し詳しく見てみよう，ということで，スライドを提示して説明します。

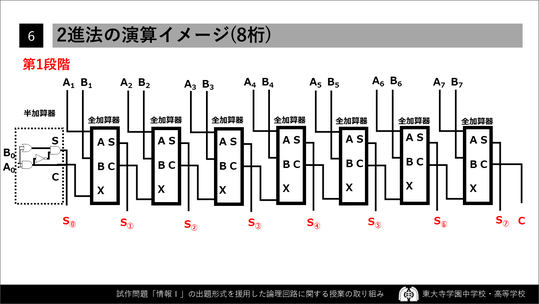
ここでは，「8桁の2進法の計算をするのであれば，半加算器と全加算器は全部で何個必要か」　と質問します。

そして，このスライドのようにS₀～S₇の8個が必要だね，という話をして，スライド左側のS₀から順にインプットして…という順番で説明していくと，生徒は改めて「ああ，なるほど」と考えを整理してくれます。

※クリックすると拡大します。

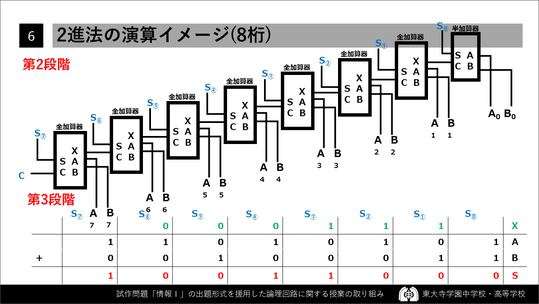
今の説明でもぴんとこない生徒には，2進法の加算の筆算は，右からしますので，演算イメージとして，こちらのスライドを見せて説明します。

第2段階と第3段階を見せながら，「こんな筆算があるやろ。そうしたら，今度は右から入ってくるものとして，こうなっていくんやで」と説明します。

これも，しばらく考えさせる時間を設けると，生徒は日頃の計算との接点を見付けてくれるようになります。この辺りは，スライドで見せることで，随分と思考の手助けになるのかなと思っています。

※クリックすると拡大します。

試作問題にチャレンジ　～問題を解きながら「なぜ学ぶのか」を理解する～

こうしたことがCPUの中で演算装置として行われているいうことが分かれば，普段はここで終わりですが，皆さんもご承知の通り，試作問題に面白い視点がありましたので，これを生徒にやらせました。

配点は6点だけでしたが，日常生活との接点を想起させ，かつそれが担っているものを学習することができる良問だと思います。

旅客機のトイレのランプで，トイレが2つの場合，両方とも使用中の場合はパネルのランプが点灯して，満室を知らせる。トイレを3つに増やして，2つ以上が使用中になったら混雑を知らせるランプを点灯させる，という条件で，該当するものを真理値表から選択させるという問題です。5分くらい時間を取って「初めてみんな試作問題するやろ。落ち着いてな」などと声をかけながら解かせました。生徒一人一人に当てて答えてもらったのですが，皆良くできていて「すごいな，よくできたね」と話しています。

日常生活の中で論理回路が使われているケースを考えてみる

ここからが一番の肝となる活動です。自分の学習と日常とをいかに結びつけるかが大事だと思っているので，私の話は15分くらいにして，残りの時間で，「生活の中で，論理回路が使われているケースを考えてみよう」という課題を出しました。

さらに，そこで考えたものを，実際に基本論理回路を用いて図示してみよう，ということにしました。この「基本論理回路を用いて」というところが，生徒には悩ましいところでもあったようです。生徒の解答をいくつかご紹介します。

生徒たちの解答例　～日常生活における論理回路の活用を実感～

ある生徒は，普段使っている自動改札機について「お金があるか，区間内か，期限内か」で考えて書いてくれました。きちんと日常生活に当てはめることができています。

次はなかなか正当派の例ですが，「1階と2階にスイッチがある階段の電灯」を考えてくれました。この生徒は真理値表も書いてくれたのですが，実は彼は感想に「3つの組み合わせだけで日常のさまざまな機能が作られていることに感銘を覚えた」と書いてくれていますが，コメント欄の最後には，XORと書いてあるのです。XORのことをわかりつつも，基本論理回路を使ってという課題の条件に従っており，いろいろ組み合わせて，付き合ってくれたのはなかなか面白いなと思いました。

「ガスの元栓が開いているか，開いていないか」がA，「ガスコンロのスイッチ」がBで，アラートが鳴るか，鳴らないかを考えてくれた生徒もいました。単純なものをいかに簡単に表現するのかということで，良い例だと思います。

「果物の選別はこんなふうにしているんじゃないか」ということを考えてくれた生徒もいました。色，重さ，大きさで，商品として合格・不合格が考えられているのではないか，というもので，つかみ方は大ざっぱですが，「世の中には論理回路が多く利用されていることがわかった」と語ってくれているので，意図は伝わってるのかなと思います。

番外編もあります。国際連盟の議決方法を，AND回路を駆使して，原則全会一致でないとダメ，というのをうまく表現しています。

結果と考察です。

実習は，基本論理回路だけで考えようとするものでしたが，生徒から提出されたものの真理値表をみると，NAND回路などになっているものが，たくさん見受けられました。

まさに，このタイミングで，生徒にNAND回路やNOR回路，XOR回路を示し，これらの汎用性の高さを実感させるのです。

さらに，AND，NOT，ORの考え方について，数学と情報の他分野との関連性についても紹介します。つまり，この実習は，学習を転移させるおもしろさを実感させたい授業なのです。

身の回りの電子機器などは，このような論理回路がたくさんに利用されていることがわかったと思います。身近な製品に対して，ユーザ目線だけ利用するのではなく，どのような仕組みで作られているのか，もちろん，全てがわからなくとも今回のような論理回路の存在を思い出してみることで，モノの見え方が豊かになってくるのではないかと思います。

最後に，何度も言いますが，この論理回路の授業を演算の仕組みの学習だけに終わらさないようにしてください。

これらの回路を使って設計したものについては，回線配置利用権として知的財産権を持つことになります。つまり，他人に勝手に模倣されないという保護期間(10年)が設定されます。

半導体を確保することも大切だし，これらの設計図をきちんと権利化することも大きなビジネスにつながっていることも理解しておくと多様な視点で物事を見ることができるようになると思います。

■質疑応答

Q-1-1.公立高校教員

数学の「論理」との関連性はどのように話されているのでしょうか。

A-1-1.𠮷田先生

数学との関わりについては，中高一貫校ということもあり，数学の進度も速いので，私は私でやっていくという形になっています。生徒は「ああ，情報と数学はつながっているんだな」というのを自分たちで導き出しているような恰好です。

Q-1-2.公立高校教員

私も，日常と情報のかかわりを密接に結びつけることは大事だと思っているのですが，実際は日常生活では，２値論理では判断できないことがたくさんあります。その辺りのところで，もし授業で生徒におっしゃっていることがあれば教えていただきたいと思います。よろしくお願いします。

A-1-2.𠮷田先生

先ほどご紹介できなかった生徒の感想の中に「数量が離散的ならば，頑張ればかなり多くのものが論理回路で表現できることが分かりました」という，教師が喜ぶような一言を書いたものがありましたが，確かに閾（しきい）値をどこで設けるかとかいうのは悩ましいところです。ですから，あまり深入りはしないようにはしていますが，入り口まではサポートする感じになっています。

Q-2-1.公立高校教員

回路と日常との関わりというところで，非常に参考になりました。私も実践してみたいと思います。質問なんですけれども，回路とコンピュータの構造との結びつきについて，コンピュータってかなりブラックボックスになっていて分かりづらいので，コンピュータがどう動いているのか，ここを回路と結びつけるのが非常に難しく感じております。何かその辺りでヒントになるようなことがあれば，教えていただきたいと思います。

A-2-1.𠮷田先生

コンピュータのプログラミングの章でやっていますので，流れとしてはこの前段階で，5大装置のことだとか，CPUの中のこと，演算や制御の話はしています。その上で，次の授業で演算の話に入るようにしています。

第16回全国高等学校情報教育研究会全国大会(東京大会) 口頭発表より