事例295
重回帰分析の学習を可能にする授業教材の提案
大阪電気通信大学高校 岸本有生先生

まず背景からお話します。データサイエンスは、新しい学習指導要領では、小学校から高校、大学を通して学ぶこととなり、注目されています。「情報Ⅰ」でも、データ活用の観点からデータサイエンスを扱っています。
問題は「情報Ⅱ」です。「情報Ⅱ」を採用する学校が少なくて、せっかくデータサイエンスで機械学習を含めた高度な内容を取り上げていても、学ぶ機会がほとんどない、というのが実態です。
今回は、授業で重回帰分析を取り上げた実践をご紹介します。実際とても難しい内容ですが、それをいかに簡単にするかを考え、導入につなげられたらと思います。
授業に必要な教材としては、まず分析ツールがあります。これは具体的にはExcelやPython、Rなどです。次にサンプルデータ、そして授業用スライドです。現状では教科書にあるものを使うことになりますが、入手可能なサンプルデータは非常に少なく、一方教科書は複雑な言い回しが多くて使い勝手がよくありません。こういった現状の中で、「情報Ⅱ」で重回帰分析を扱うために、これらの必要な教材を準備してみました。

単回帰分析の応用として重回帰分析を学ぶ
まず、授業提案のポイントは3つです。
重回帰分析は、「情報I」で学ぶ単回帰分析を応用したものです。「気温が上がればアイスクリームが売れる」という相関があれば、その応用で重回帰分析ができます。生徒には、まずそこを理解させます。
また、重回帰分析には難しい専門用語がたくさん出てきますが、今回は導入なので、できるだけ使用しないようにしました。
さらに、単回帰分析では予測の精度が低かったものが、複数の説明変数を使うことにより、予測モデルの精度が良くなるということを理解させます。例えば「成績を上げるための適切な勉強時間を知りたい」というときに、単に勉強時間だけでなく、もともとの成績や今までの勉強時間など、複数の要素が関わってきますが、では何が一番効いているのかはわかりません。実は他にも関与する要素があるのではないかということを調べられるのが、重回帰分析です。

こちらがイメージ図です。
「気温が上がればアイスクリームが売れる」というのが単回帰分析です。
それに対して、重回帰分析では複数のデータを組み合わせることで、新しい予測ができます。場合によっては未来予測もできる。重々しい名前の割に、とても楽しいものなのです。

「Connect DB」でまず単回帰分析をやってみる
具体的な進め方です。まず、単回帰分析を、大阪電気通信大学の私たちの研究室で開発したConnect DB(※1)というソフトで行う方法をご紹介します。
Connect DBは携帯電話でも使用可能です。水色のアイコンをクリックすると、ソフトが起動します。
※クリックすると拡大します。
まずサンプルデータを選びます。ここでは、「アイス・お茶の売り上げ数」で、気温とアイスクリームの売上数を予測するという活動をやってみます。
※クリックすると拡大します。
このサイトには、サンプルデータとして様々なデータが仕込まれています。
「アイス・お茶の売り上げ」の画面の中で、緑色のバーから「アイス売上数」と、一番端の「気温」にチェックを入れて、左上の「方法」ボタンで、「単回帰分析」を選択します。
※クリックすると拡大します。
すると、横軸が気温、縦軸がアイスクリームの売り上げの散布図が出てきます。相関係数は0.86でやや右上がりに見えるので、左上の「回帰直線の式を表示する」のボタンを押すと、回帰直線を引くことができます。
※クリックすると拡大します。
回帰直線を入れたグラフがこちらです。
回帰直線の式から出てきたアイスの売り上げは、
184.3545+93.2321×気温[℃]
となります。ここから、気温に対して傾きが93ということで右上がりであること、他にも決定係数が多く精度が高いことなどが読み取れます。
※クリックすると拡大します。
Connect DBのトップページではログインを求められますが、サンプルデータを使用する場合は、ログインなしでも使用可能です。またログインすると、例えばGoogleフォームのような使い方や、csvデータでデータベースを作っておいて、必要な時に分析に使うこともできます。
マンションの家賃と説明変数の関係を散布図行列で見る
次に題材にしたのは、同じくConnect DBに入っている「家賃(重回帰)」のサンプルデータを使ったマンションの家賃の予測です。駅までの時間、築年数、面積、階数などのうち、どの説明変数が家賃に影響するのかを考えます。

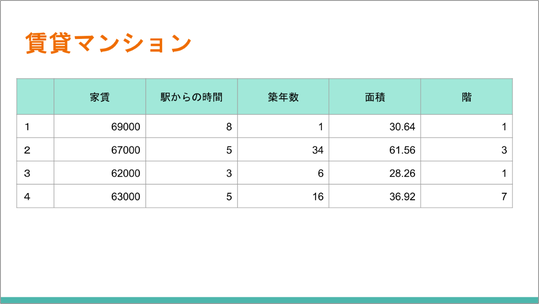
こちらがデータのサンプルです。
家賃を6万円代のものについて、駅からの距離、築年数、面積、階数を記載しています。広いけれど築年数が経っているもの、あるいはその逆などもあります。
このデータを生徒に見せると、いろいろな感想が出てきますが、あくまでも肌感覚でしかありません。
このたび、ConnectDBに散布図行列と重回帰分析の機能を追加しました。
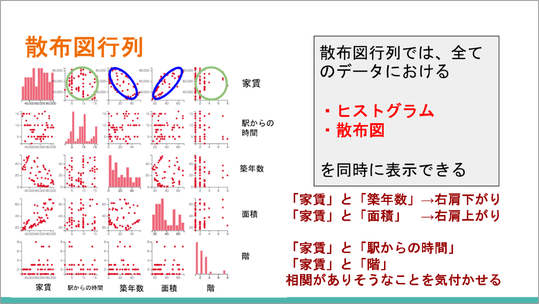
「散布図行列」では、全てのデータ間のヒストグラムと散布図を同時に表示することができます。

分析の方法です。サンプルデータの中から「家賃(重回帰)」を選びます。
説明変数で、「家賃」「駅からの時間」「築年数」「面積」「階」を選択し、「方法」で「相関分析」を選択します。
※クリックすると拡大します。
家賃と「駅からの時間」の単回帰分析の結果がこちらです。
駅から近いと、家賃が高いときもあれば安いときもあり、あまり相関がないということがわかります。イメージとしては、駅から近いと家賃が高そうですが、そうとは限らないことが実感できます。
このソフトの大きな特徴は、結果がうまく出なかったときは簡単にやり直せることです。やり直したい時は、×ボタンで戻ることができます。
※クリックすると拡大します。
次に家賃と「築年数」、家賃と「面積」について回帰分析してみます。すると、「築年数」には負の相関が、「面積」には正の相関があるように見えます。
※クリックすると拡大します。
個々の説明変数と家賃との関係を一つひとつ見るのは大変なので、サンプルデータのページで家賃から全部チェックを入れて「散布図行列」を押すと、スライドのようになります。「情報」の大学入学共通テストのサンプル問題にも、このような散布図行列が出題されていましたね。
ここで、家賃に対して各説明変数がどのような関係があるかを一度に確認することができます。
※クリックすると拡大します。
重回帰分析で家賃を予測してみる
さらに、重回帰分析を行います。
「方法」で「回帰分析」を選択します。予測に使用する説明変数が2つであれば単回帰分析、3つ以上であれば自動で重回帰分析になります。
これで、説明変数から家賃を予測してみます。
※クリックすると拡大します。
まず、「駅からの時間」と「築年数」で家賃を予測してみました。横軸は重回帰予測値です。
サンプルデータの値から、重回帰分析の式を当てはめて予測の点を作り、それに対して実際の家賃がいくらだったかを比較しています。
説明変数が複数であっても、散布図のバラつきが大きく、決定係数も0.28程度と、予測の精度はあまり高くないことが見て取れます。
※クリックすると拡大します。
今度は、全ての説明変数にチェックを入れてやり直してみると、決定係数が0.948と、精度が高くなりました。
駅からの時間がマイナスになるほど家賃は減っていくことを右上の式の赤い文字で示しています。同様に、築年数が増えれば家賃が減ることを赤字、面積が増えれば家賃が上がることを青字で示しています。
※クリックすると拡大します。
今度は、説明変数を「築年数」と「面積」に絞ってやってみます。すると、決定係数は0.9418です。全ての説明変数を使った際の決定係数が0.9481でしたので、殆ど変わりありません。
これは、先ほど全ての説明変数を使ったときは不要で影響力の低いものが含まれていたことを示します。ここで影響力が低かったのは、「駅からの時間」と「階」でした。このように、説明変数の選び方を試行錯誤することで、必要なものの取捨選択ができるということです。
先ほどもお話ししたように、Connect DBは、予想して試してみた後に少し違うなと思ったら、変数を消したり増やしたりしてやり直しが何回もできる、試行錯誤に適したツールになっています。
※クリックすると拡大します。
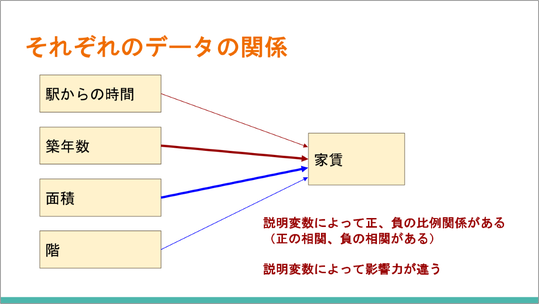
全体の関係をまとめます。
家賃に対して、「駅からの時間」と「階」は影響力が小さく、「築年数」と「面積」は影響力が大きいことがわかりました。
赤で書いた部分は負の、青で書いた部分は正の相関、比例関係があります。分析の結果を、このような図を書かせてまとめさせるのも良いと思います。
サンプルデータの設計についてです。
先ほどは家賃の話で進めましたが、高校生にとっては家賃よりももう少し身近に感じる題材があると良いと思います。彼らには、初めから知らないことを考えたり予測したりすることは難しいからです。
今回の家賃の話は、この金額であれば住みたいか・住みたくないかという話としては、何とか身近なものとして成功しているかなと思います。
また、複数の説明変数のすべてにチェックを付けるような単純操作ではなく、必要なものを取り出すために考えさせて、その上で取り組めるような題材があるとよいと思います。

大学生による授業実践では…
最後に、大阪電気通信大学工学部の2年生149人に対して行った授業の実践をご紹介します。
旧課程の学生ですから、高校で「データ分析」はあまり学んできていません。ですので、最初の90分間は気温とアイスクリームの売り上げを使って単回帰分析を説明し、その後先ほどの家賃データで散布図行列や重回帰分析を利用して、どのようなことが分かるか、という授業を行いました。

重回帰分析の理解度のチェックはこのような形で行いました。
まず、散布図行列からデータの回帰分析や相関の特徴を読み取れるか。次に、家賃が安くなる説明変数を見つけることで、回帰直線の正負を読み取れること。そして、重回帰分析に利用するデータ変更して、影響力を調査することができること、という3つの課題を設定しました。

散布図行列からデータの特徴を答える課題では、右肩上がり、右肩下がり、相関の有無など、特徴を読み取れているかどうかを確認します。
正解率は77.9%と、8割近い学生が理解できていました。

次に、家賃が安くなる傾向に影響する説明変数(課題2)と、重回帰分析に利用しても影響力の低い説明変数(課題3)を探す課題を行いました。
正解率は課題2が79.9%、課題3が最も正解率が高く85.2%でした。

最後に、理解できたことを自由記述してもらった結果がこちらです。
複数のデータから、さらに正確なデータを予測できることを知った」重回帰分析では影響力の小さい値は省いても問題がなかった」という感想は、こちらの意図をつかんでくれていることがわかります。

今回は、専門的な知識を全く持たなくても重回帰分析を学習できるようなソフト開発を行い、実際の授業で使ってみた結果、ほとんどの学生が理解できました。重回帰分析のおもしろさを実感できる導入として、「情報Ⅱ」や、「情報Ⅰ」の応用編としてやってみていただきたいと思います。
質疑応答
Q1.私立大学教員
私は、かつて多変量分析をExcelでやらせたことがありますが、まず可視化するときに、3変量であったときに軸を増やして、xyzの座標系で図示することができるのでしょうかということ。もう一つは、分析手法の方では、アソシエーション分析など、さらに高度な手法と関連付けていかれるのかということ。この2点について、うかがいたいと思います。
A1.岸本先生
ありがとうございます。最初に、3変量の図示について。これは、どちらかというと、グラフ化するというよりも、予測精度が高いか・高くないかということを見るのが中心で、グラフ化まではやっていません。
さらに高度な手法ということについては、ここである程度基本的な考え方、概要を押さえて、できれば次につなげていきたいと思います。
Q2.私立高校教員
最初の単回帰分析のアイスクリームの話で、スーパーの店長の立場に立てば、来週の予想気温が高いからアイスクリームをたくさん仕入れよう」という、未来の予想に使えそうな気がしました。先ほどの家賃の問題については、生徒にこの分析の結果をどのように生かせる可能性があると考えていらっしゃいますか。
A2.岸本先生
例えば、自分が不動産屋のオーナーだったとして、この地区でマンションを建てるのであれば、家賃設定はどうしたらよいか考えるときに使えるね、という感じですね。これは、家賃の設定をする側の気持ちに立たなければならないので、生徒には実感が湧きにくいかなというところはあります。ただ、彼らの中にもこのくらいの家賃であれば住みたいか、住みたくないかというのはあるので、一応いけるかなと思います。
他にも、実際ノートパソコンの機能と値段の関係という例も作ってみましたが、なかなかいい結果が出なかったので、今のところはこの家賃の例を使っています。
第16回全国高等学校情報教育研究会全国大会(東京大会) 口頭発表より