事例322

1.「論理回路」が全てのスタート→2進での足し算のしくみ

まずは、「論理回路が全てのスタート」ということで、論理回路の展開についてお話しします。

最初に、中学校の復習として、コンピュータは2進法で表されたデータで処理していること、そして実際どのように計算を行っているのかの種明かしをします。そして、教科書を使って、AND、OR、NOTなどの用語について、それぞれ集合と理科の回路を例に挙げながら説明します。

ANDゲート(論理積ゲート)はこのような形で、これは集合で言えばAとBの両方が「1」の場合のみ、「1」を出力する。電気の回路で言えば直列のスイッチの配置と同じであることを説明します。

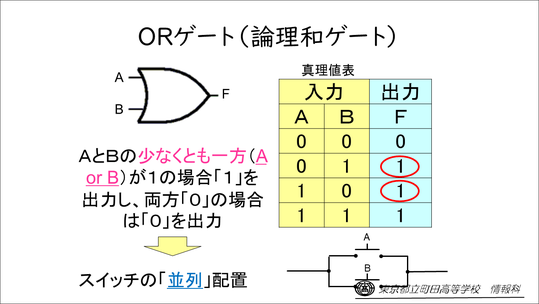
ORゲート(論理和ゲート)は、集合のORと同じで、AとBの少なくとも一方が「1」の場合に「1」を出力し、これは並列のスイッチの配置と同じです。

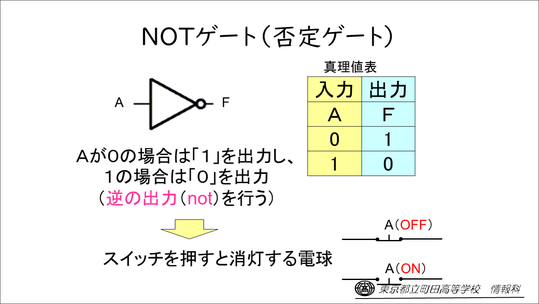
また、NOTゲート(否定ゲート)は、Aが0の場合は「1」を出力、1の場合は「0」を出力というように、逆の出力をします。これは、スイッチを押すと消灯する回路と同様です。

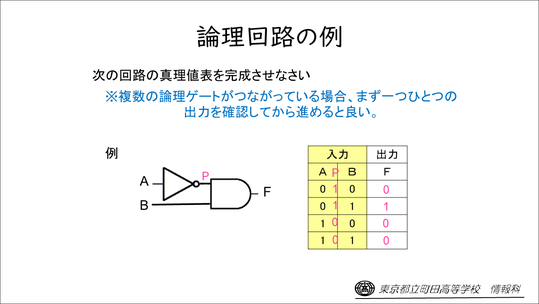
これらを確認し、副教材の練習問題に取り組ませた後、実際に複数の論理回路を簡単につなぎ合わせたもので真理値表を完成させます。

こちらは、接続点をPと置いて、AとBにそれぞれ1または0を入力した場合、まずPではどうなるか、最後の出力Fはどうなるか、一つひとつ段階を追っていくとわかりやすいよ、と指導しながら、真理値表を埋めていきます。

その後に、実際に副教材を使って練習問題を行います。

これは自分たちで考えさせた後、一人ひとり順番に当てながら、出力が0か1かを答えさせていくスタイルで行います。

2進法での足し算の仕組み

次に、いよいよ本題の2進法で実際どのように足し算をしているかを見ていきます。

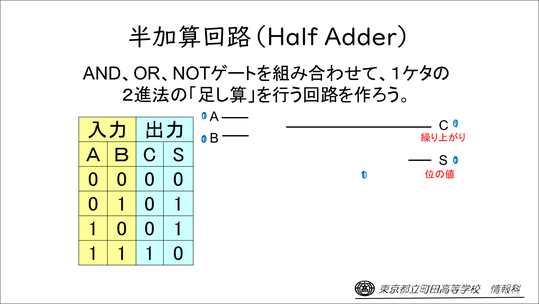
2進法の足し算はこの4パターンしかありません。

これを入力2つ、出力2つの真理値表に表し、それぞれの入力に対応するように出力されれば全自動の2進法計算機になることを見せて、これを回路で作ろう、ということを説明します。

実際に入り口を2つ、出口を2つ用意して、AND、OR、NOTゲートを組み合わせて半加算回路を作っていく作業を行います。

繰り上がり「C」は、AND回路がそのまま使えるので簡単ですが、位の値「S」はなかなか難しい。

※クリックすると拡大します。

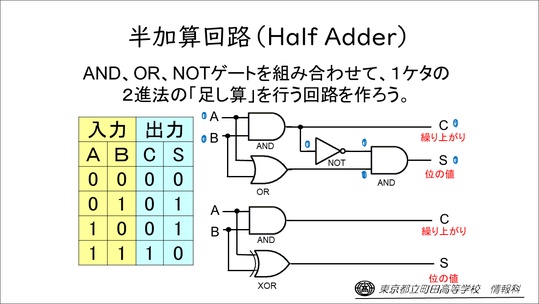
そこで、ここでは答えの回路を先に出してしまって、実際にそうなるのか、一つひとつ0、1と入れてこれを生徒に答えさせながら、確かにこうなるね、ということを確かめていきます。

そして、「それぞれの入力に対して、それに対応するような出力になったということは、スライドのようにつないでいけば、全自動2進法計算機ができる。今はゆっくり説明しているけれど、実際のコンピュータの中では、電気なのであっと言う間に結果が出てくるんだよ」という説明をしています。

※クリックすると拡大します。

また、このままではつなぎ方が複雑なので、大学の教科書や専門書では、AとBのうちどちらか一方だけが1のとき1を出力する「エクスクルーシブOR(排他的論理和（XOR))」が使われていることが多い、という話もしています。

※クリックすると拡大します。

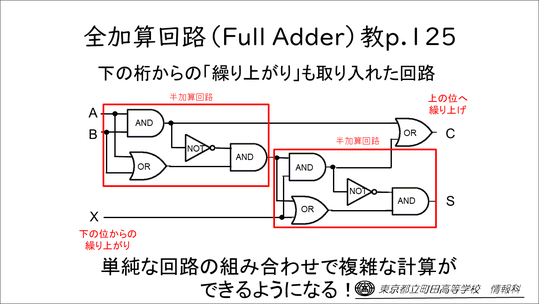
2桁以上の足し算は、小学校で習った筆算を用いて説明しています。これも手順は簡単ですが、生徒には一つひとつ確認しながら、「筆算はこのような形で前の桁の繰り上がりがあるね。2進法も同じで繰り上がりを足さなければいけない。でも、先ほどの半加算回路は繰り上がりを考慮していないから、今回は繰り上がりを考慮した全加算回路を作ろう」ということを説明します。

はじめの半加算回路で、AとBの2つの数を足した後に、次の半加算回路で、下の位からの繰り上がりを足す、という仕組みです。

上からCに来ているのは、最初の桁の2つで繰り上がったレーン。下からCに来ているのは、後から足して繰り上がったレーンで、どちらでもよいのでORになるね、という話をしています。

※クリックすると拡大します。

このように、単純な仕組みを組み合わせることで、どんどん複雑なことができます。

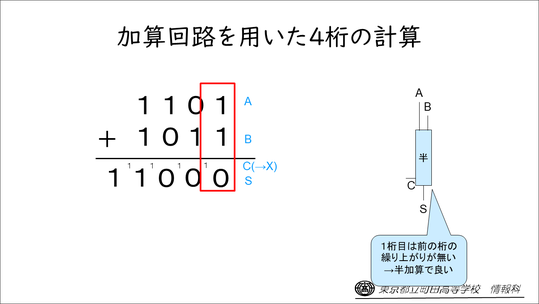
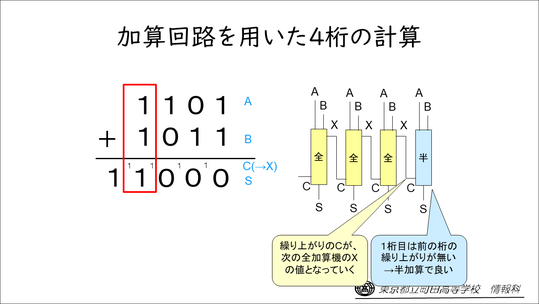
例えば4桁の計算であれば、1桁目は繰り上がりがないので半加算回路でよいけれど、2桁目からは繰り上がりがあるので、全加算回路が必要になります。下からの繰り上がりCを次の位Xにつないであげたら、次の位もその次の位も、同じように自動的に計算できることになります。

※クリックすると拡大します。

つまり、4桁の計算をやりたかったら、半加算回路1つと、全加算回路3つ。

 10桁であれば、半加算回路1つ、全加算回路9つでよいことになります。

このようにして2進法で計算ができるんだよ、という説明をしています。

※クリックすると拡大します。

※クリックすると拡大します。

２.２進での四則演算→足し算だけでかけ算・引き算・割り算を

次に、2進法での四則演算です。ここまでで足し算ができることが分かったので、掛け算、引き算、割り算はどうなるか、ということで、ここはあえて掛け算を先に行います。

なぜなら、掛け算は足し算に簡単に直すことができるので、生徒も直感的に「掛け算はすぐにできる」ということがわかるわけです。

また、別の考え方として、10進法で10倍するときは最後に0を1個付けて桁をずらしたのと同じように、2進法で2倍するときは、最後に0を1個付ければ全ての位の数が2倍になるので、同じように桁をずらすといいよね、という話もしています。

ここからが本題の引き算です。ここで「補数」について扱います。引き算をするときには補数の考え方が必要になるからです。

補数は、「元の数」と補数を足せば桁上がりをする数のうち最小のもので、元の数を「引く」代わりにその補数を「足し」て繰り上がりを無視すれば、同じ計算ができることになります。

つまり、補数がわかれば「引き算」を「足し算」に変えられることになります。

しかし、10進法で補数を求めるときには一般的に引き算を使っているので、これはおかしいよね。引き算は使えなかったんだよね、ということに生徒に気付かせます。

そのため、10進法の場合はうまくいかないのですが、2進法では、NOT回路を使えば、0と1を簡単に反転させることができます。

これと元の数を足せば、必ず1＋0か0＋1なので、全ての桁が1になり、さらにそれに1を足せば、桁が繰り上がります。つまり、「元の数の0と1を逆にして1を足したもの」が2進数の補数であることが簡単に分かるよね、ということで、「2の補数」に誘導します。

実際に2進数の補数を求められるようになったら、補数を用いた引き算を体験させ、練習問題も行います。

こちらも一つひとつ実際に生徒に解かせながら、最後にマイクを回して一人ひとりに答えてもらって、答え合わせをする、という形で行います。

さて、最後に割り算です。割り算は、元の数の中に割る数がいくつあるか、ということですが、生徒は意外にこのことに気が付いていないケースが多いです。

例えば、35÷9をどう考えるか、というと、多くの生徒の解答は、おそらく九九の逆算で、9×3＝27、9×4＝36となる。4は無理だから、商は3で、35－27で、余り8と。

確かにそのとおりですが、実はもっと単純に「35の中に9が幾つあるのか」ということなので、9を引けるだけ引いていけばよいことになります。

ここでは3回引けたから、答えは3。残ったのが8だから、余りは8と考えればよいことになります。

 こうすることで、割り算を引き算に直すことができます。

引き算は、すでに前のステップでできることが分かっているので、これで足し算だけの考え方だけで、掛け算、引き算、割り算が全てできたことになります。

4.アルゴリズムの基礎→順次:差　反復:積　判断:商

最後に「4.アルゴリズムの基礎」です。「3.計算の限界」は、今回は省略します。

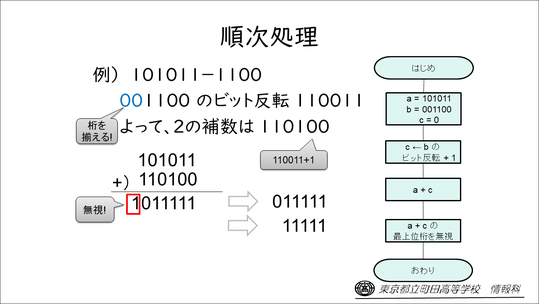
こちらは、引き算の順次処理のフローチャートですが、先ほどの補数を用いた引き算が、実は一直線の順次処理でできていることを示します。

※クリックすると拡大します。

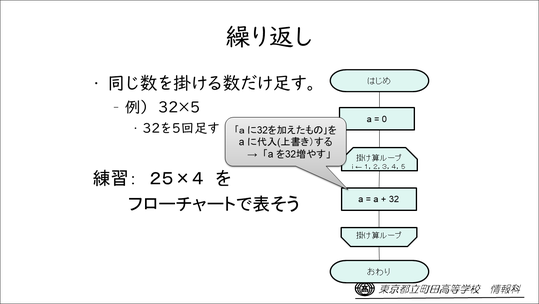
繰り返しについては、これは掛け算のフローチャートです。

32×5であれば、32を5回足せばいいので、5回繰り返しています。

そのとき、a＝a＋32という式がポイントですね。いわゆる「上書き」です。
「『aに32を加えたもの』をaに代入(上書き)する→aを32増やす」
という代入の式の意味について、「これまで皆が使ってきた計算式とは、＝(イコール)の意味が違うんだよ」ということを、ここで丁寧に説明します。

※クリックすると拡大します。

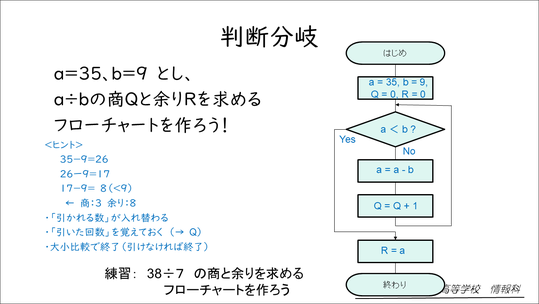
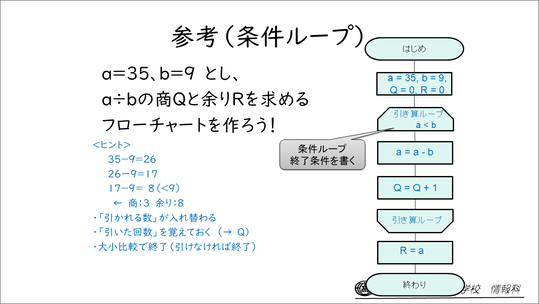
さらに判断分岐を扱います。ちょうどこれが割り算とぴったりマッチします。なぜなら、「まだ引けるかどうか」という判断を行って、引けるところまで引いて、引けなかったら、そこで終了して余りを出すことになるからです。

このような形で、実際に生徒に他の数字でのフローチャートを考えてもらった後に、「他の数字での割り算フローチャートを考えるときには、初期の部分[「はじめ」の次の部分］だけ入れ替えればよい。つまり、私たちはその後に続くこれらの処理の流れを考えればいいんだよ」という誘導をしています。

※クリックすると拡大します。

条件ループも、ここで簡単に扱うこともあります。

※クリックすると拡大します。

「しくみ」から入り、同じ題材で同じことを応用させ、「遊び心」を大切に

ここまで説明してきたことをまとめます。

アルゴリズムの説明はストーリー性を持った流れで行い、単純なことの組み合わせでできる、ということを説明しながら進めていきます。

そして同じ題材を使うこと。この実践で言えば、四則演算という同じテーマを繰り返して何回も行うことによってイメージしやすくなります。

また、最後にアルゴロジックを入れたり、好きなものを作ったりといった、知的好奇心や遊び心を大切にした授業を展開しています。詳細は、こちらの私のサイトに上げておきましたので、ご覧いただければと思います。

「情報科準備室～小原研究室」

神奈川県情報部会実践事例報告会2023オンライン　オンデマンド発表より