高校教科「情報」シンポジウム2019秋

学習11「コンピュータの仕組み」

まず、学習11「コンピュータの仕組み」です。

その中で、『コンピュータの構成と演算の仕組み』は、主として知識問題になるかと思います。次の『AND・OR・NOT、真理値表』は、いわゆる論理設計、論理回路の話なので、このあたりは面白い問題がたくさん作れますが、実際高校の授業でどれだけできるのかというのはわかりませんし、おそらくそれほど深く学ぶ時間はないだろうと考えています。今回用意しているのは、割合簡単な問題です。

三つ目が『計算誤差、プログラミングを使った計算誤差の確認』です。この誤差について、教員研修資料の記述は、個人的にちょっとどうかなと思っています。15ビットの箱に13ビットの魚は入るけれど、20ビットの魚は入らない、これが誤差の原因だという図があります。

これは多分、オーバーフローの話をしているのだと思いますが、そうであれば、容器に水を入れていって、容量を超えるとまさにオーバーフローするよという例のほうが、直感的にわかりやすいのではないかと思うのですが。

この誤差というのは、この章の非常に重要なポイントです。コンピュータが計算の対象にできるのは、先ほどの図にあったように、有限集合にマッピングすることができるものだけだということです。

例えば整数であれば、32ビットならプラスマイナス20数億の範囲を表現できます。しかし、通常の整数の対応のさせ方以外に、例えば偶数だけを対応させてもよいし、10、20、30…とやってもよい。あくまで有限の集合に対応させれば、どのようにも扱えます。

一方、実数の場合はどうなるのか。実数は、どの2数を取ってもその間に無限に数が存在するので、そもそも有限集合にマッピングできません。そこで誤差が生じるわけです。数直線上でも、ある範囲のものを一つの値としてマッピングせざるを得ないのです。1.1とか0.1を2進数で表現すると、この数直線のある範囲の中の1個の点を代表しているわけで、そこには必ず誤差が生じます。それが積もり積もっていかないように気をつけないといけないねという話です。この辺りが重要な点かと思います。

学習12「外部装置との接続」

学習12『外部装置との接続』は、計測・制御、センサ、アクチュエータの話です。中学校の技術科でも行うことになっていますが、ここは、ぜひ高校の授業でも実習していただきたいと思います。

教員研修資料にはmicro:bitの例が示されていますが、入試を考えたときには特定の教材に依存した問題は非常に出しにくいので、抽象化せざるを得ないだろうと思いますが、ここについては適切な問題はまだ用意できていません。

教材としてはmicro:bitやArduinoがよく使われますが、いずれもワンボードマイコンで、それ自体で独立したコンピュータになっています。図で言えば、左側が通常のOSを含んだコンピュータで、実際にmicro:bitなどを使うときには、これらをUSBでつないでダウンロードします。その場合、図の左側のOSから見れば、右側のmicro:bitもデバイスの一つですが、接続を切り離すと、右側のmicro:bitは独立したコンピュータであって、通常のコンピュータと入出力装置の関係ではありません。

つまり、このmicro:bitのプログラムを作るときは、micro:bit 上のLEDやアクチュエータの入出力専用のコンピュータとしてのプログラムを作成します。一方、いわゆる汎用的なコンピュータの下で入出力装置として使おうとするときには、ディバイスドライバーなどが関わってくるので、かなり難しい話になってきます。授業では、おそらくそこまでは踏み込めないと思います。

学習13「基本的プログラム」

学習13「基本的プログラム」では、『アルゴリズム・プログラム・フローチャート』『順次・分岐・反復』『変数』について扱います。この章では、繰り返しと条件分岐を組み合わせて自力で簡単なプログラムを書けるようになることを目指して欲しいと思っています。

ここはいろいろな問題を作ることができると思いますが、ポイントとしては二重ループのプログラムを書けるかどうかではないかと思います。

教員研修資料には、フローチャートの話が書いてあります。逐次と条件分岐と繰り返しという三つの基本構造が載っていて、これを組み合わせてフローチャートを書く、ということです。そのとき、書き方に気をつけないと、変な構造になってしまいますよ、というのがこの図です。

右から二つ目の図には「START」と「END」とあって、この赤い印のところに、左の三つの基本構造のどれかを埋める。埋めた基本構造の中の赤い印のところに、さらにこの三つのどれかを埋める…という形で作っていけば、きれいな構造のフローチャートができますが、それをきちんと意識せずに書いていくと、右端にあるようなアンストラクチャードな構造になってしまいます。

 フローチャートを使って指導するときは、今お話しした手順で作成できるフローチャートのみを対象にすることを心がけていただきたいと思います。

学習14「応用的プログラム」

学習14「応用的プログラム」では、『配列、乱数、関数、WebAPI』が扱われています。

まず配列が取り上げられています。教員研修資料では、リストと書かれていますが、中身は完全に配列について説明しています。

Pythonのリストというのは、非常に便利でいろいろ高度な機能が使えるデータ構造ですが、便利な機能に踏み込んでしまうと、Pythonと他の言語とでは様子が違うことになります。教員研修資料では、この点に配慮して、Pythonではあるけれども、他の言語と共通である配列の機能に限定した説明がなされているものと推察しています。

そもそも、授業でプログラミングの学習にどれくらい時間がかけられるでしょうか。私の想像では、せいぜい10時間かと思いますが、では10時間でどこまでできるか、ということになりますね。我々が大学の授業で、非常に基本的なところ教えるのに、だいたい4コマ＝8時間分使っていますので、おそらく高校でもそのくらいでしょう。

10時間ではせいぜい配列までだと思います。リストのいろいろな機能をやろうとしたら、ちょっと大変だなと思いますので、その意味でせめて配列ぐらいまでは頑張ってほしいと思います。

関数に関しては、自分で定義できるかということと、利用できるかということが問題ですが、どちらかというと、利用することの方が簡単ですし、いろいろな機能の高い関数をいくつか用意して、それを使ってプログラムを書け、ということになると、プログラムの記述量を減らせるので、面白いことを短いプログラムでできる可能性があります。そういうところは、ぜひ授業でもやっていただきたいですし、試験にも出しやすいかなという気がします。

その延長上で、Web上にリクエストをあげて、計算結果をもらってきてプログラムを組もうというのがWebAPIです。おそらく、この研修資料の作成者側は、ぜひこれをやってほしいと考えていると思いますし、私も同感です。

ただ、これは入試問題としては非常に出しにくい。仮にCBTで入試を行う場合、クローズドなネットワーク内にサーバーをおいて、そこに疑似的なWebAPIを用意するということはできなくはないですが、いわゆる本当のインターネットにダイレクトにつないだ入試というのは、セキュリティの面からちょっと考えにくいです。

学習15「アルゴリズムの比較」

学習15「アルゴリズムの比較」では、探索アルゴリズムの比較とソートアルゴリズムの比較の話が書かれています。いわゆるアルゴリズムの計算量、つまりどれくらい時間がかかるかという問題です。

ここについては、大学で研究している人がたくさんいますので、いくらでも高度な問題は出せますが、入試問題として適切なものというものはなかなか難しく、せいぜいソートアルゴリズムが上限ではないかと思っています。

実は、この部分の教員研修資料に間違いがあります。研修資料の選択ソートとクイックソートを比較した部分で、『クイックソートでは、逆順に並べ替えられている場合など、ある条件下では比較を行う回数が膨大になり…』と書いてありますが、実は逆順に並んでいる場合に比較回数は大きくならないです。スライドの一番下の数列は、今は大きい順に並んでいますが、これをクイックソートでやると一番後ろの90と一番前の10を交換します。次は80と20、次は70と30…と1回さーっとなめたら、全部入れ替わってきれいに並びます。ですから、「逆順に並んでいたら膨大な比較回数が必要」というのは誤りです。

同じ効率の良いソートアルゴリズムでマージソートというのがありますが、こちらの方がずっと簡単ですし、どんな場合でも0(n log n)で並べ替えができて、「クイックソートでは比較が多くなる場合があるよ」などという議論すらいりません。クイックソートはあまりやらない方がいいかなという気はします。

学習16「確定モデルと確率モデル」

確率モデルはいろいろなところで出てきます。銀行の窓口とか切符売り場、あるいはエレベーター、電車等の待ち行列や交通渋滞、信号機の点灯時間の長さの調整などでシミュレーションが使われているので、その中から適切な問題を考えればよいのですが、今回はなかなかうまく作れていません。

シミュレーションのプログラミングで作題する場合、何が難しいかというと、シミュレーションのモデルを作るときには、基本は並行動作です。ですから、並列に動きうるプログラミング環境では比較的簡単にプログラムを書けるのですが、多くのプログラミング環境、プログラミング言語は逐次処理で動きますから、シミュレーションのプログラムを書くのは一般に簡単ではありません。そういうわけで、作題も難しいということです。

簡単な例として、銀行の窓口にお客さんがやって来て、待ち行列に並んで、窓口が開いた方に順番に処理するというものがあります。

このとき、お客さんが順番にやってくる所が一つあって、三つの窓口がそれぞれ独立にあって、並列に動作しているというモデルが一番わかりやすいですが、窓口と関係なくお客さんがやってくるというプログラムと、窓口1・2・3のプログラムが別々にあって、それぞれが同時に動くというモデルではいろいろ工夫が必要になるので、プログラムは簡単ではありません。そういう意味もあって、まだ具体的な問題作りができてない状況です。

学習17「自然現象のモデル化とシミュレーション」

食物連鎖というのは、イノシシはヘビを食べて、ヘビはカエルを食べて、カエルは虫を食べる…という中で、カエルの数が少し減ったらどうなるか、というものです。こういったシミュレーションはよくありますが、具体的にどんな問題を作るかということになります。残念ながら今回は作問例はありません。

　※以下、ダウンロード問題は「高校教科『情報』シンポジウム2019秋」の予稿集から引用しています。

こちらは簡単な10進法と2進法の変換の話で、10進法を1桁表すのに何ビット必要かという問題です。これは簡単なところですね。 

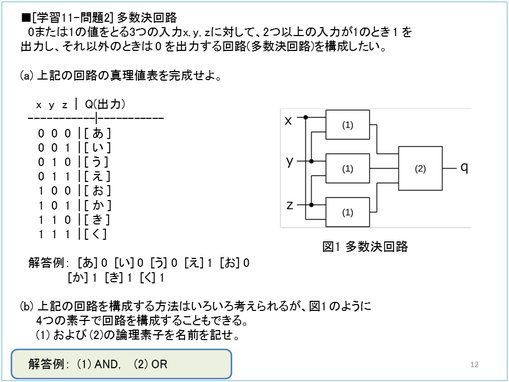
問題11　コンピュータの仕組み　作題例

こちらは論理回路の多数決回路の構成の問題です。(a)が真理値表の完成で、(b)が回路図でANDかORかあてはまるものを選ぶ、という問題です。これも易しい問題です。 

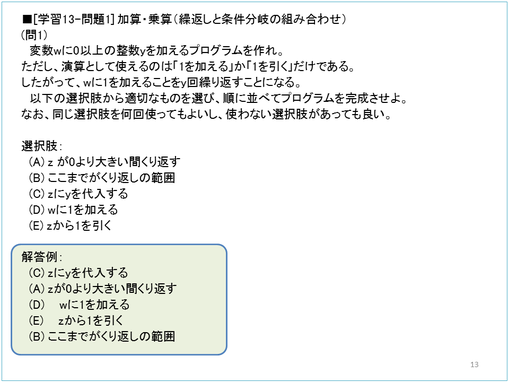
学習13　基本的プログラム　作題例

加算と乗算を「1を加える」と「1を引く」というオペレーションだけで実現するという問題です。

つまり、「wにyを加える」という計算は、wに1を加えることをy回繰り返す、ということです。これは用意された選択肢を順番通りに並べる、という形で解答を要求しています。

下図は、前の問題の問2に相当するもので、「xにyを掛ける」という計算のプログラムです。解答例の青い部分が、先ほど問1で作ったプログラムで、「zにyを加える」というプログラムをここに使って、さらにそれをx回まわす、というものです。これも選択肢を並べ替える形で解答します。

学習13　基本プログラム　作題例

『1～1000の整数のうち、3で割ると2余り、かつ、4で割ると1余る整数の合計を計算する』というプログラムを作るもので、穴埋めではなく一から書く、という感じです。短冊を用意していますが、ほとんど自分で埋めることに近いです。ループの中に条件分岐が入っていますが、このようなプログラムをぜひ自力で作れるようになってほしいと思います。 

この問題を、CBTで実施したときのイメージが下図です。右側に選択肢が並んでいて、左側に順番に並べてプログラムを構成して実行してみるというものです。

学習14　応用プログラム　作題例

数式処理の問題です。(  )などを含んだ複雑な数式を作る際に、関数定義を正しい順番で呼び出すというものです。 

学習15　アルゴリズムの比較　作題例

最大値と最小値を両方求めるときの手間数の問題です。最大値を求めるためには、整数がn個あったら、少なくとも(n－1)回比較しないと求められません。最小値も同様に、(n－1)回の比較が必要です。

 それでは、最大値と最小値の両方を見つけるなら、単純に考えたら(n－1)回の2倍で求められますが、もう少しうまくやる方法があるよね、というのがこの問題です。

学習16　確定モデルと確率モデル　作題例

これは学習16のシミュレーションの問題です。

教員研修資料には、円周率を求めるためのモンテカルロ法のサンプルがあったので、それを単純にy＝x*xとx＝1とx軸とで囲まれた部分の面積を求めようとしただけで、問題としてはほとんど同じで、要するに定積分を行っています。 

学習16　確定モデルと確率モデル　作題例

これは40マスあるすごろくを、サイコロ1個を繰り返し振っていくつで上がるかのシミュレーションを行う関数sugoroku1()と、それを1000回繰り返した際にあがるまでの回数の分布をリストに記録する関数test()のプログラムです。

後半、ちょっとややこしいことになっていますが、コメントがありますので、それを見て何をしているのか理解はできるのではないかと思います。 

一番下の行が、サイコロを振った回数ごとに上がった回数です。0回から6回では当然上がれない。8回振って上がれることが1000回のうち13回あった、という結果です。平均的には、だいたい10～11回で上がれているというところです。

このシミュレーションを修正するというのが、下図です。前のプログラムでは40ぴったりでなくても上がることはできますが、(a)は、ぴったりでない場合はもとの場所にとどまるように変更するものです。

→(sugoroku2)

(b)は、ぴったりでない場合は余った数のぶんだけ出発点の方向に戻るというもので、これが一番一般的なルールですね。

→→(sugoroku3)

(c)は、10・20・30にコマが止まったら振り出しに戻るというものです。

→→(sugoroku4)

情報Iを学んだらこんなことができてほしいなと思いながら、作問してみました。皆さんのご意見を伺いたいと思います。

高校教員Q1:学習指導要領では、アルゴリズムの表現が「文章、フローチャート、アクティビティー図」となっていますが、実際はフローチャート一辺倒で、何とかならないかと思うのですが、これについてはいかがでしょうか。

竹中先生A1:専門教科情報の学習指導要領を読んでいただくとわかると思いますが、アクティビティー図や状態遷移図、それからDFD(データフロー図: Data Flow Diagram)といったものも出ています。先ほどのお話にもありましたが、新指導学習要領では、難しいコードを書くことが目的ではなく、要件定義から単体プログラムを作り、それをマージして一つの情報システムを作り、そしてテストを経てリリースするまでの流れを体験しましょう、というのが基本的な流れになっています。そういう意味で、フローチャートという単体的な話だけではなく、データの流れや状態遷移がどうなっているのかというところをUI(User InterfaceやUX(User Experience)も含めて学びましょうと、書いてあるはずです。つまり中学校技術科が計測・制御をシステム的に捉えるということを考えるので、その上位として高等学校にもそれが繋がると思います。

大学教員Q2-1:学習13の問題1・問題2についてです。問題1「加算・乗算(繰り返しと条件分岐の組み合わせ)」の問1(変数wに0以上の整数yを加えるプログラム)は情報Iでもできると思いますが、問2(0以上の整数xとyに読み込み、その積を計算して表示するプログラム)はできるでしょうか。

問1は簡単です。問2は問1が二重ループになっているだけかもしれませんが、そこがはたしてわかるでしょうか。

高校教員Q2-2:私の学校は、一応進学校に分類されていますが、かなり上位者でないと理解できないと思います。理由は、うちの県だけかもしれませんが、今の生徒は、ものをイメージしたり想像したりする能力がとても弱いので、こういった問題を読んで二重にループするという状況を想像するのがとても難しいと思います。

それをするために、教員が例えばフローチャートとか何か資料を準備する必要があって、その上でこれが難しいか簡単かというのは授業のやり方かなとは思いますが、単に問題に答えると結構難しいという印象があります。問1の方は、さすがにできると思います。

松浦先生A2-2:これは、見かけはややこしそうに見えますが、実は極めて単純なループなんてすが、基本的に二重ループがしんどいということなのでしょうか。

高校教員Q2-3:そうですね。二重ループの概念がなかなか理解できないというか、イメージがつかないということがあると思います。

松浦先生A2-3:多分、そこは非常に重要な分岐点だと思います。少なくとも、情報Iでは二重ループぐらいはやってほしいなというのは、私の願いではあります。

高校教員Q2-4:先生の言われた「やってほしい」という気持ちは私もありますが…、

大学教員Q3:「CBTのイメージ」というイラストで、何となくどのように当てはめていくのかがイメージできましたが、その前の学習13の問題の図では、そもそもこのプログラムが入れ子になっていることが見えませんでした。

解答例にはインデントがついていますが、インデンドはたぶんわかっているからつけるのであって、インデントがなかったら、繰り返しの終わりがどこか、判断できるののかなと思いました。これがCBTのイメージの図を見ると、例えば5から7がスコープになっているとか、4から9が対応しているっていうのは、見たらわかりますが、だぶん文章だけではわからないだろうと思いました。

あと、学習13の問題2で、n%3=2という式が、私たちはこれが「3で割った余りが2」と勝手に変換しますが、問題をそのまま読んで数式を書かせたら、表現があまりにも自由に許され過ぎていて、採点するときかえって大変ではないかと思いました。

松浦先生A3:確かに、「プログラムを作れ」という課題を出す限りにおいては、いわゆる文法の定義は明確に決まっていなければならないですね。そこら辺りについて、まだ明確な方向性が見えていません。今ここではほぼDNCLで書いていますが、CBTで行うのであれば、この図では色をつけていますが、ループの構造がわかるような工夫が当然あるべきだと思います。

また、今回の設問はかなり端折っていますので、「%は剰余演算を示す」といったことは当然書いておくべきだと思います。制御構造はどう書くかということについても、当然何らかの指示は必要ですが、その言語の資料が明確に公開されてないと使えないのは確かです。おっしゃるとおりです。

高校教員Q4:私は二重ループは高校生に教えたことはありませんが、実は数学で今、非常に深刻な状況が起こっていて、Σや漸化式の計算のイメージがつかめないのです。本校では、シグマ計算をRで同じようなことをしていて、そのとき必ずΣの話と漸化式の話をペアにして話していますが、そもそものΣの計算と漸化式の考え方がまだ定着していなのです。ですから、先ほどの二重ループというのは、どの程度のものかリアリティーはありませんが、も数学の授業の実態から考えると、かなりハードルは高いなというのが今の感想です。一つフィックスして他の一つを動かすというのがかなり厳しいです。

松浦先生A4-1:一つ言い訳するとするならば、今現在の高校生ではなく、2025年の高校生向けの問題を考える必要があるということです。ですから、それぐらいの授業をしてほしいというところはあります。

大学教員4-A2:二重ループに関しては、将来的には小学校・中学校でプログラミングを体験した子が、高校でこれを習うという前提だと思っています。中学校の技術科でも二重ループが出てきますが、それはこの問題のような数理的なものではなくて、ループの中でセンサの値を受け取って、ロボットに何かをさせるといった文脈が、普通に教科書に載るような教材の準備が進められています。反復の中に分岐があって、その中に反復があるというのが普通に出てきます。

ただ、そこでは二重ループだからといって、iとjという複数の変数の値が変化するところまで扱っているわけではないので、その辺がやっぱり高校の難しいところで、全く新たに出てくるところかなとは思います。ですから、二重ループだからどうだ、と一括りにしてしまうと、議論がちょっとおかしな方向に行ってしまうかなと思いました。

竹中先生A4-3:中学校の計測制御の中でも結果的にシステム的思考を扱います。二重ループに関しては、現在の専門教科情報の教科書にはたくさん入っています。

また、私が高校でC言語の授業をやっていたときに二重ループを扱った課題が出てきましたが、九九の問題とか、アスタリスクを積み上げてピラミッドにするとかいった問題は、普通科でもできたので、あとは授業のやり方次第と思います。

現在の中1の子たちからは新しい要領で学びますので、これからの中学校・高校の学びに期待していくべきかなと思っています。

高校教科「情報」シンポジウム2019秋　講演より