高校生のためのコンピュータサイエンスオンラインセッション2020
コンピュータサイエンス×手芸×デザイン
五十嵐 悠紀先生 明治大学 総合数理学部 先端メディアサイエンス学科
コンピュータサイエンスの力でオリジナルぬいぐるみの型紙を作る

今日はコンピュータサイエンス、それから手芸、デザインといった観点からお話ししたいと思います。
まず、簡単な自己紹介です。私は、2005年にお茶の水女子大学理学部情報科学科を卒業しました。その後、前回お話をいただいた萩谷先生がいらっしゃる東京大学の情報理工学系研究科のコンピュータサイエンス専攻を修了して、2010年に工学系研究科で博士号を取得し、理学学士→情報理工学修士→工学博士と、理学から工学までちょっとずつ移り変わってきたバックグラウンドを持っています。

私自身は手芸が大好きですが、自分でぬいぐるみをデザインするのはとても難しいんです。なので、キットを買ってきたり、本に載っているものを使ったりして作っていたのですが、やはり自分でデザインしたものを作りたい。でも素人がデザインをするというのは大変なので、そこに情報科学の力を組み込むことで解決する、ということをやってきました。今日はこのお話を簡単にご紹介したいと思います。

自分だけのオリジナルぬいぐるみを作りたいと思ったとき、何となく3次元を思い浮かべることはできると思います。ぬいぐるみなんて作らないよ、という方は、ペーパークラフトでも思い浮かべてください。
何か立体なものを作るためには、まず平面、つまり2次元の型紙を用意しなければならず、それ自体難しいですが、型紙がたとえあったとしても、その出来上がりの形状は縫ってみないとわからない。そこで普通は、専門家がデザインしたものをキットとして買ってきて作るということをしていると思います。
うさぎのぬいぐるみを作りたいけど、くまの型紙しかないとき、くまの耳をうさぎの耳のように大きくして作ったこともあります。ところが、縫ってひっくり返して綿を詰めてみたらすごく細長い耳ができてしまった。縫って、綿を入れて膨らませた後の形がどうなるかという、そんな単純な形でさえ出来上がりを予想するのは難しいのです。
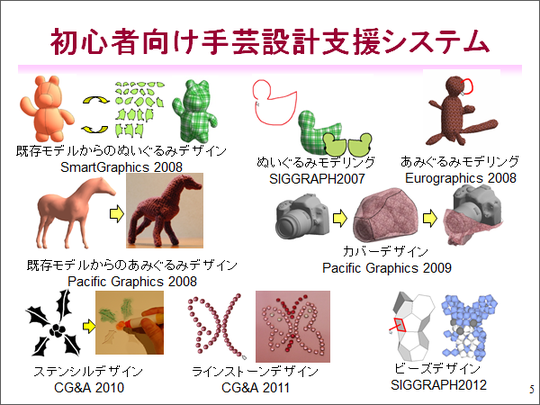
私は、コンピュータグラフィックスや、ユーザーインターフェースといった分野の研究者ですが、修士や博士のころから、今お話ししたような分野の観点から、情報科学の力を借りて、初心者向け手芸設計支援システムを作ってきました。手芸って、情報科学とはかけ離れた分野のことに思われるかもしれませんが、そういった異分野コラボレーションの例として、楽しんで聞いてもらえたらと思います。
縫って綿を詰めたシミュレーションをCGで作る
今までいろいろなことやってきましたが、今日はその中で、分かりやすい身近なものを4つ取り上げてご紹介したいと思います。

まず、ぬいぐるみです。ぬいぐるみは、自分でデザインするのは大変ですが、これをコンピュータでデザインします。自分で外形を線で描いて、その型紙をコンピュータが作り、縫い合わせたシミュレーションをします。

動画をご覧ください。
右側が型紙で、左側はそれを縫って綿を詰めた3次元の立体になっています。縫い合わせた結果が3次元の赤い線にフィットするような型紙になるように、右の型紙のほうがもぞもぞ動いています。ユーザーがコンピュータでデザインしている間に、裏でシミュレーションを動かしているわけです。
普通の3次元モデラーを使うと、切断面は平面やスイープ面になってしまいますが、これは中に綿を詰めたシミュレーションをしているので、立体になっています。突起を付けたいなら、ユーザーが突起の形状を描いたあとサムネイルを提示してくれます。
腕や足のような太ったパーツ、耳やしっぽのような、ぺちゃんこのパーツをそれぞれ提示してくれます。また、つまんで引っ張りたいときには、型紙の方をちょっと修正するなど、3次元の形状を操作していくだけで、型紙もそれに合わせて徐々にできていきます。線を追加で入力したり、引いた線によって縫い目が多くなってきたらコンピュータの中で型紙同士をつないだりすることも行います。
また、例えばペンギンのおなかをちょっと出っ張らせたいときには、型紙を左右非対称にすることもできますし、ダーツを入れて膨らませるということもできます。ぬいぐるみ設計士さんは、経験や専門知識がたくさんあるので、やりたいことに合わせた新たな型紙を作れますが、このシステムでは、私たちはデザインに集中している間に、コンピュータがぬいぐるみになるような3次元モデルを作ってくれて、そのモデルができたときには、実際に型紙も合わせて作られているということになります。
こちらができた型紙を縫い合わせて作ったぬいぐるみです。油性ペンとかで色を塗って仕上げました。

こちらは、バルーンの製作会社さんに声を掛けていただいて、こういった大きなバルーンも創っていただきました。こういったバルーンもぬいぐるみと同じく、設計士さんが結構大変な思いをしてデザインされているんですけれども、このシステムを使うと手軽に作ることができます。

また、大学での研究は、論文を書いたり特許を出したりということで終わることも多いですが、最近ではユーザースタディー、いわゆるフィールドワークといって、外でワークショップをやったりすることもよくあります。2006年に東京のお台場にある日本科学未来館でワークショップを行ったときの様子が動画にはのっています。子どもたちに自分だけのオリジナルぬいぐるみを作るということを体験してもらって、コンピュータでいろんなことができるんだよ、ということを紹介しました。
コンピュータの中の仕組みをちょっとだけ説明すると、入力した線が真四角だったとき、同じ形の型紙を使って縫い合わせをすると、シミュレーション結果は上段の真ん中の緑のような、皆さんの枕や座布団のような形になります。
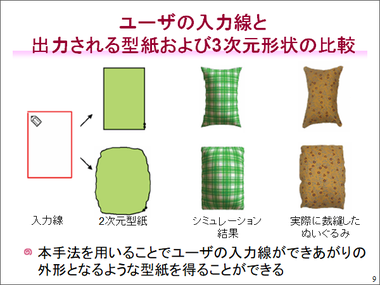
しかし、ぬいぐるみで欲しいのは縫い合わせた結果が真四角になることですから、縫い合わせた結果に合わせて少し膨らんだ型紙を用意することが必要です。そのために、コンピュータの中で何度も何度もシミュレーションをして、計算結果を得るということを行っています。
実は、3次元モデルは、頂点と辺と面の三角形の集合で表されています。その頂点を、ベクトルや法線といった、高校数学で聞いたことがあるようなものを使って外側に膨らませていく、といったことを行っています。

複雑な形のカバーの制作にも応用できる
次にカバーデザインの紹介をします。身の周りにはいろいろなカバーがありますが、このカバーを自分でデザインしてみるには、結構制約が大きいです。

まずは、包み込めないといけないですよね。それから、取り出し口から取り出すことができなければいけない。これは当たり前のようですが、それを満たすような3次元形状をデザインして型紙を作るのは結構難しいです。コンピュータを用いて、これらの制約を解くということをやっています。

カメラカバーを例にお話しします。カメラにはCADモデルがあるので、そこから始めています。それにconvex hullつまり、凸包という形状を計算して、カバー形状としています。カバーが本体を包み込める大きさになるように、縮まらないで展開できる方法とか、取り出し口をデザインしたときに、そこから取り出すことができるかのシミュレーションの方法を提案しています。

動画をご覧ください。こんな感じでシミュレーションして、取り出すことができる、OKだね、ということをシステム内で確認してから、実際に型紙を縫うことを行っています。3次元を包み込むような型紙を作るには平面に展開することが必要ですが、平面展開は必ず歪みが生じます。
例えば、地球と世界地図を思い浮かべてください。メルカトル図法とかモルワイデ図法とかいろいろな図法がありますが、面積をなるべく等しく展開するか、あるいは2点間の距離をなるべく等しく展開するかなど、いろいろな制約を最小にするという方法で2次元に展開されます。

例えば、今ここに出した円筒や円錐形のように、伸縮することなしに平面に展開することができる曲面のことを、数学的にはガウス曲率がゼロの面とか展開可能な面ということで、可展面(Developable surface)と呼ばれます。

一方、通常の3次元モデル、つまりいろいろなところが出っ張ったり凹んだりしている状態なものを展開すると、縮む所と広がる所が出てしまうんですね。
下図は、発泡スチロール球を4分の1にカットしたものを、布で包んだ様子です。この3次元の表面をよく使われる角度ベースの手法、Angle Based Flatteningで展開したもので、布で覆うとちょっと発泡スチロールが見えているところもあるし、余ってしまっている所もあることがわかります。

発泡スチロールがすべて見えなくなるまで拡大させると、余っている所はもっと余ってしまいます。これは単純な図形なので、別に余ってもかまいませんが、誤差がたまっていくことでいろいろな影響が起きてしまいます。
赤い辺が縮んでしまっている辺、青い辺が伸びてしまっている辺、緑の辺が元の3次元形状の辺の長さとほぼ同じ辺とカラーリングしていますが、私たちの方法では、縮む辺がないような展開手法ということを提案して、必ず包み込むことができるという制約を解決しています。


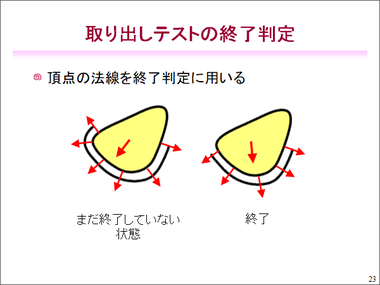
次に取り出しテストを紹介します。実際に縫ってみて、取り出そうとしたら取り出せないのではいけないので、あらかじめ取り出せるかどうかをシミュレーションします。

このカメラの例では、物に対して入口が小さ過ぎるので、何となく気付けますが、例えば赤ちゃんの服をデザインするときを考えると、赤ちゃんはけっこう頭が大きいのですね。だから、首周りが頭よりも大きく開くように作らないと、着ることができなくなってしまいます。そういった知識がいるようなデザインを、実際に作る前にコンピュータでシミュレートして取り出せなければデザインを修正するといったことができます。
取り出しテストの終了判定には法線を使っています。法線がいろいろな向きに向いてたら、まだ終了していませんが、全ての法線が90度以内、つまり内側に向いていたら、取り出すことができる、という計算をコンピュータの中で行うことで、取り出すことができる・できないを判定しています。
ビーズのデザインも一筆描きの応用でCGで作れる
次にビーズデザインです。ご覧になったことはありそうですね。2次元のビーズだと、ドット絵のような形で並べて絵を作ります。最近は霧吹きをしたらくっつくアクアビーズとか、アイロンの熱でくっつくアイロンビーズとかも販売されています。

でも、このスライドにあるような3次元の立体のビーズは、おしゃれですが実は作るのは大変で、右側に表示しているようなレシピと呼ばれる図を使って作ります。これは1本のワイヤーで作られていますが、真ん中の赤い三角のところからスタートしてます。1本の糸を、右側が赤、左側が青と分かりやすく左右で色を変えていますが、1個のビーズを糸が左右から通っていて交差をするように作っていきます。最後に糸をぎゅーっと引っ張ると、中心付近にある黒いビーズが飛び出して、目と鼻になってくまの顔の部分ができる、そんなイメージです。
これを作る時、平面のレシピを見て作るのですが、手元には糸でつながって3次元になったビーズのかたまりができていて、ちょっと休憩したり、続きは明日やろうといったことにしたりすると、どこまでやったかすごくわかりにくくなってしまって、私自身、なかなか最後まで作ったことがなかったような題材でした。
このビーズを、どう研究するのかお伝えします。このビーズモデルは、全て4mm角で同じサイズのそろばん型ビーズを使っていますが、このビーズを辺に対応させることで、「全ての辺の長さが等しい多面体を作る」という問題に置き換えることができます。何か情報科学っぽくなってきましたよね。

こちらも動画で説明します。
全ての辺の長さが等しい正多面体には、いろいろな形があります。そういったものを多面体で作っていく、というのをコンピュータで解かせます。正多面体や準正多面体をマウスホイールで選んでいったり、面を選択してスイープすることで、その飛び出させた頂点の位置をコンピュータで計算することもできます。頂点から頂点につないでそこの辺をなくしたり。
そのほか、辺をクリックすると、辺が分割するなど、ジェスチャーインターフェースを使って、「ここに辺を入れたい」「頂点をなくしたい」という情報をユーザーから与えていきます。そうすることで、コンピュータは裏側で「ここに辺を入れるんだね。入れるんだったら、辺の長さが全部同一だから、こんな形だね」というシミュレーションをして、全ての辺の長さが等しい多面体になるように変形してくれます。
このシステムは色を付けることもできます。3次元形状でデザインしたものを、3次元のまま制作手順を提示するということをしました。これによって、目の前に見えているものと、実際に手元に出きた、3次元のビーズが1対1対応するので、途中までやって休憩してしばらく手を休めても対応がすごく取りやすいので、中学生に向けてワークショップをしたときも、作り終えることもできました。
多面体の図とビーズモデルの図と、実際に作ったビーズの写真がこちらです。ビーズの個数、ようするに辺の個数は66、77、96。一番右のくまさんは、実際のビーズを買ってきて、それを見ながら自分でデザインをしてみました。大体、100から200~300くらいなら作り終えることができるかな、という印象です。

コンピュータの中の話をすると、先ほどの一番上のデザインモデルと、一番下のビーズ作品モデルの間に、実は構造モデルといって、シミュレーションのための複雑な内部構造を持つポリゴンモデルを使っています。

デザインモデルの辺の長さを全部ビーズに対応させてるのですが、裏側では実はビーズエッジとワイヤーエッジっていう二つのエッジ、つまり辺にさらに分割しています。
そして、ビーズに対応する所を頂点、ワイヤーの所を辺と考えて、頂点(ノード)と辺(リンク)のグラフを作ります。これはグラフ理論という分野ですが、こういったグラフというものを作ることで、一筆書き理論というオイラーグラフに持ち込むことができます。
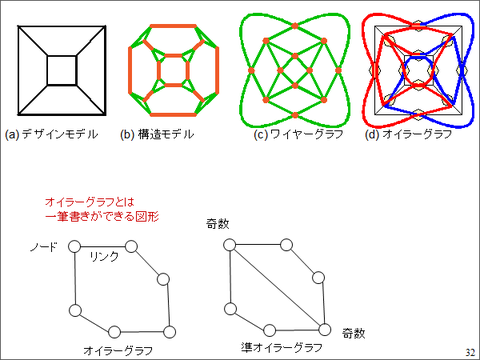
一筆書きを簡単に紹介すると、一筆書きができる図形をオイラーグラフというのですが、ノードとリンクを考えたときに、ノードから出るリンクの数が全て偶数本だったらオイラーグラフとなって、どこから始めても一筆書きができます。この例の場合は全てのノードからリンクが2本ずつ出てますね、こういったオイラーグラフを作ることで、1本のワイヤーでビーズ作品を作ることができることになります。
もう一つ、準オイラーグラフというものがあって、これは2カ所だけ奇数で、あとは全部偶数というものです。これも一筆書きができますが、奇数のどちらか一方からスタートして、相手方の奇数でゴールをするというルートしかかあり得ません。奇数が3個目があったり、1個しかなかったりしたら、一筆書きができません。

つまり、1本のワイヤーで全てのビーズを回ってきたいので、こういった構造モデルからオイラーグラフを作って、それを解くということを内部的に行うようにしました。
ところが、実際に作ってみたら大変でした。指示通りにワイヤーを通していくと、押さえられなくてワイヤーがぷらぷらしてしまいます。それを可視化すると、このスライドのような状態です。

つまり、固定されている(stableな状態の)ビーズと、ピンクのようにぷらぷらになっている(unstableな状態の)ものがあるわけです。最終的にワイヤーがぐるっと回ってきて、最後に閉じると面ができて固定されるのですが、ぷらぷらの状態のままいってしまうと、手で押さえておいたり、セロハンテープで止めたり、誰かに持ってていてもらわないといけないわけです。
実は、オイラーグラフというのはどこからスタートしてもよいので、解、つまり答えがいっぱいあるんです。ですから、たくさんの解の中から最初に見つかった答えが、製作に一番適しているとは限らないので、製作している間に不安定な状態になるビーズが、最小限になるように、ワイヤー経路を計算するということを計算で求める必要があります。

そうするために、他のビーズ作品をたくさん観察して、全ての面を1個ずつ終わらせていけばよいことがわかり、そのアルゴリズムを考えるにあたっては、ハミルトンパスという、グラフ上の頂点を1回ずつ全部回っていくというグラフ理論を使って、すべての面を1つずつ終わらせていく、という手法をとっています。
そうすることで一個一個の面をしっかり終わらせて、不安定なビーズがなるべく少ない個数で済むような、オイラーグラフというものを作ることができています。

ラスタ方式×ベクタ方式でステンシルの型紙を作る
最後に、ステンシルのデザインの話をしたいと思います。ステンシルは、型があって、その上からインクをのせていくことでデザインするアートです。クリスマスのとき窓に考えて型を置いてスプレーを吹き付け、取ってみると絵ができていますよね。あれと同じです。これをデザインするのは結構大変なのです。

私は里帰り出産したときに、実家で新生児用の真っ白な服に何か刺繍をしたいな、と思ったら、母に止められました。「赤ちゃんの肌は弱いので、縫い目が直接肌に当たらないように外側に向いているんだよ。だから、刺繍で糸や縫い目が肌に当たるようなことをしてはいけないんだよ」ということを聞いて、じゃあステンシルしよう、と。
私はくまが好きだから、くまのステンシルしよう、なかなか好きな型がないな、じゃあステンシルの型を作ってみようと、お絵描きしてたら、これがすごく大変でした。1枚につながった状態で絵を描くって、どうしたらいいんだろう。これでは耳が取れちゃう、とかいうことをしているうちに、コンピュータに解かせたらいいじゃないかと、里帰りをしているのに、ひたすらプログラミングをしてしまうことがきっかけで、この研究が始まりました。このように、研究の種がどこにころがっているかわからないということも、知ってもらえたら面白いなと思います。
ユーザーが絵を描くと、コンピュータが1枚につながっているという制約を解いてくれて、白い紙の中に黒の所が抜け落ちるような絵が描かれます。黒と白の領域の境目をトレースして、それをカッティングプロッターで切り取ることで、型紙ができます。これに色をのせていきます。ユーザーは、お絵描きをしていくだけで、白い紙の中に黒い所が抜け落ちていく感じです。

これには、普通にペンで書くモードと塗りつぶしモードがありますが、それを組み合わせて絵を描いたりくっつけたり、描いた後に順番を入れ替えてあげることもできるので、描いたものを手前側にしたいとか奥側に変えたいとか、やはりちょっと動かしたいということもできます。描いているうちに、内側が抜け落ちてしまうときには、自動で橋渡しをしてくれますし、不要になったら橋は消えます。こんな感じで1枚につながるという制約を全部コンピュータが解いてくれて、自分で好きなようにお絵描きをしていくだけで、ステンシルを作るということができる、というものです。
コンピュータの中はどうなっているか、見てみましょう。2次元の画像には、画素データの集合で表されるラスタ形式と、図形の座標軸で表現されるベクタ形式という2つの形式があって、どちらにも利点と欠点があるので、そのときによって、どちらを使うかを自分たちで決めて使うわけですね。
例えば、写真はラスタ形式ですし、パワーポイントはベクタ形式で作られています。

このステンシルソフトの中では、入力ストロークは全部ベクタ形式で行っているので手軽に移動したり、コピペしたりできますが、内部的にはラスタ形式としてboolean処理、つつまりtrueだったらtrueといった真理値で表しています。つまり、1枚につながるという制約を満たすために、両方の形式を持っているというわけです。こうして、自動的に「島」となる部分を検出して橋を生成する、ということを行い、コンピュータの中で1枚のつながった絵にするという制約を解いています。

駆け足になりましたが、手芸作品のデザインを自分でやりたいと思ったときに、結構難しいところを情報科学の観点から支援してあげて、初心者や子どもたちが、設計や製作を楽しむことができるようなツールを、研究し、提案してきました。

それを実際に使ってもらうワークショップも、いろいろな所でやらせていただいてきました。

最近はパソコンやスマホ以外にもいろいろな機器が手軽になってきています。例えば日本の伝統工芸の木目込み細工を、3Dプリンターを使って手軽に設計支援する、ということもやってみました。

また、ストリングアートといって、釘にひもを規則的につないでいくことで美しい形を作るアートがありますが、これをシステムで設計して、LEDライト使って制作支援する、ということもしています。

また、ポンポン手芸ではどこをカットしたらきれいなひよこの形になるのかをWEBカメラを使って支援したり、フェルティングニードルでチクチク刺していくのをARグラスで、型紙と実体をうまく重ねて作り易くしたりすることにも挑戦しました。


このように、新たなデバイスがどんどん安く手軽になって、家庭用に導入されてきたら、手芸にも新しい可能性が広がります。
10年前は何十万もした3Dプリンターが、3Dプリンターも、今安いものは1、2万円くらいになっています。今から10年先には、もっと便利なデバイスが1人1台持てるようになっているかもしれない。そんな世界を見据えて、いろいろどんなことができるかを研究しています。
「○○×コンピュータサイエンス」で広がる未来
今回は様々な制約、例えばぬいぐるみが綿を入れると膨らむ、カバーデザインは必ず包める、ビーズは辺の長さが必ず一定になる、ステンシルは必ず1枚につながっている、といった中でデザインをするとき、制約は全部コンピュータに解かせて、ユーザーはデザインに注力できるようにすることをご紹介しました。

今回は、手芸とコンピュータサイエンスという観点でお話をしましたが、これまでコンピュータが入ってなかった分野に、情報科学の視点を入れることで、どのような可能性が開けるか、という異分野コラボレーションを、ぜひ自分の好きな趣味や自分の身の回りからどんどん探してもらって、自分が解決したいという分野をぜひ見つけてみてほしいと思います。
私自身が情報科学の分野に進んだのは、数学とか物理が大好きで、お茶の水大のオープンキャンパス行ってみたら、理学部の数学科と物理学科の横に情報科学科があって、数学も物理も使って、自分が好きな手芸も音楽も結び付けられる情報科学って最高の分野だ!と思ったのがきっかけです。ぜひ皆さんも、自分の趣味も伸ばして、苦手なことは、得意にならないまでもちょっと底上げして、高校生生活を楽しんでもらえたらと思います。