慶應義塾大学総合政策学部　2018年情報入試問題解説

キミのミライ発見大学入試問題研究プロジェクト

監修・執筆　間辺広樹先生(神奈川県立柏陽高等学校教諭)

日本で唯一の本格的な情報での入試選抜を実施しているのは、慶應義塾大学(総合政策学部・環境情報学部)です。18年度の問題と、解説・学習方法をまとめました。

「キミのミライ発見」サイトでは、14年からの参考試験も併せて解説も掲載しています。併せて、入試状況、その選抜で重要な小論文対策に関しての情報も示しました。

<本ページ下に案内してあります>

入試学習対策にも、情報・小論文の学習や指導にも、ご活用いただけましたら幸いです。

慶応義塾大学の湘南藤沢キャンパス（SFC）にある環境情報学部と総合政策学部では、2018年度入試において３度目となる「情報入試」が実施されました。本稿では、総合政策学部に出題された問題について解説します。

まず問題を見てみよう!

→18年度総合政策学部

→環境情報学部の入試問題解説はこちら

→「情報」入試に向けた学習法はこれだ!

全体

情報-1は、情報化社会におけるセキュリティや法に関わる問題であった。例年本大問では新しい用語とその意味を知っているかを問われる問題が出題されている傾向は続いているため、毎年政府が出している「消費者白書」などに目を通しておく必要があった。

情報-2は、論理演算、グラフ理論の最小全域木、逆ポーランド記法に関する問題であった。問題文を読み、落ち着いて情報を整理する能力が求められた。教科書に記述されている基本的な論理演算・補数表現を学習した後、誤差を実際に計算する問題や数式を表現する方法などの学習にステップアップしていくのが学習の指針としてベストであると考えられる。

情報-3は、光の三原色と色の三原色に関わる問題で、ディスプレイなどに加法混色と、プリンタなどに使われる減法混色の理解、並びにそれらを変換するための知識が求められた。これらの三原色関連の問題は初出題となったが、教科書に書かれていることを基本とし、出題されているため、少しでも多くの問題を正解し、得点源としたい問題となった。

情報-4は、左右異なる色のメガネを用いて立体的な表示を行うアナグリフという技術を用いた問題であった。特殊な技術を扱っていたため、受験生は問題文を読んで論点を理解することに戸惑ったのではないかと考えられる。

情報-5は、迷路探索のアルゴリズムの一つである深さ優先の探索法に関する問題であった。スタートからゴールまでの経路を見つけるために「とりあえずどれかの方向を選んで先に進み、行き止まりになったら戻って別の方向を試す」というアルゴリズムを実現させるプログラムの問題でもある。古典的なアルゴリズムを題材とした問題ではあるが、高等学校レベルを超えた難問であった。

以下、大問ごとに解くためのポイントを解説する。

情報-1

(ア) 不正送金被害を防ぐためには、マルウェアなどが仕掛けられている可能性がある共用パソコンなどは使うべきではない。したがって、(4)が誤り。

(イ) 指静脈認証は指の内部の静脈を使用するため、触れた場所の残留物などから形態を再現することは困難である。したがって誤りは(5)。

(ウ) 正解は(２)。著作法は著作物を「思想又は感情を創作的に表現したもの出会って、文芸,学術,美術または音楽の範囲に属するもの」と定義しているため、アイディアは著作権お保護の対象にはならない。プログラムは基本的に著作権による保護となると形式的な暗記をしている場合、(2)を選択してしまう傾向にある。表現に創作性が認められるか否かが著作権として認められるか否かの焦点にあたることを見直しておきたい。

(エ) 商標権の存続期間は登録日から10年で、更新も可能である。したがって、正解は(２)。

(オ) 個人情報事業者が利用目的を変更することができるのは、人命や財産保護に関わるなど特別な状況のためだけに認められるものである。したがって、誤りは(２)。

(カ) 情報公開法の背景には、政府はその活動を国民に説明する義務を負うという考え方がある。したがって、正解は(５)。

(キ) 基本料金は無料で、高度なサービスには課金をするようなビジネス手法をフリーミアムモデルという。したがって、正解は(３)。

(ク) 「自然変動を支持する少数グループ」にとって、自分たちの主張を「必要以上に大きく」取り上げてくれるバランス報道は「よいバランス」と評価するであろう。したがって、正解は(4)。

情報-2

（ア）集合とその論理演算に関する問題である。まず、集合であるから、つぎのような式が成り立つ。

また、論理演算は、数の足し算や掛け算のように分配律などの法則が成り立つ。

従って、論理和と論理積の組合せ問題は次のように整理できる。

この考え方を使えば、一見複雑な問題もわかりやすい形となる。

（イ）頂点と辺から構成されたグラフの最小全域木を求める問題である。様々なアルゴリズムがあるが、ここでは『「頂点Aから他の頂点までの距離の最小な頂点とそこに繋がる辺を選ぶ」ことを繰り返して、すべての頂点に繋がる道を作る』というアルゴリズムを用いる。グラフの問題は、条件を満たすグラフを描くとよい。以下に最小全域木が作られる過程を図示する。

求めるグラフSは、A-B-D-C-G-F-H-Eの順で辺と頂点を追加しながら最小全域木が構成された。頂点CがSに加わるときは、Vtに含まれているのはE, F, Gの3点だけである。また、完成したSにおいて、頂点Aからもっとも距離が離れている頂点はEであり、その距離は１０（＝4+6）である。

（イ）は演算子を数値などの被演算子の後ろに書く記法の一つであり、例えば「４＋５」であれば「４　５　＋」の順で書く。この記法は「４と５を足す」という日本語の語順とよく似ている。

解答を求められている「１２　５　＋　４　×」は「１２と５を足して、４を掛ける」、すなわち（１２＋５）×４となり、計算すると６８、

「３　１２　＋　４　６　＋　×」は（３＋１２）×（４＋６）となり、計算すると１５０となる。

逆に（１２＋４２）×２１は、「１２　４２　＋　２１　×」、

３６／（６＋８）は「３６　６　８　＋　／」となる。

情報-3

色の表現方法について、情報の教科書でも扱われている光の三原色と色の三原色の知識を問う問題である。

光はRGBすなわち、赤（R）、緑（G）、青（B）の３つの光源を使った加法混色では、光源の強さを変えることで目的の色を作り出す。これはディスプレイなどで使われる。一方、色はシアン（C）、マゼンタ（M）、黄色（Y）の色材を使った減法混色では、色材の濃さによって目的の色を作り出す。これは、カラープリンタなどで使われる。

加法混色はそれぞれの色の発光体が出す光を混合する。一方減法混色はその色が反射しない色材を混合することによって色を作り出す。例えば、マゼンタと黄色を混ぜ合わせると赤に見える。加法混色と減法混色は相互の関係になっていて、まとめると次のようになる。

光の三原色を使った加法混色による表現を、色の三原色を使った減法混色に変換するには、この表から考えればよい。

例えば、加法混色で赤は(R,G,B)=(9,0,0)と表すが、減法混色で赤を表すには、マゼンタ＋黄色であるから、(C,M,Y)=(0,9,9)となる。このことから、以下が成り立つと予想できるが、実際に正しい。

C = 9 – R, M = 9 – G, Y = 9 – B

したがって、加法混色の(R,G,B)=(2,4,9)は、上記の変換式を当てはめて、(C,M,Y)=(7,5,0)となる。

情報-4

右に赤色、左に青色のフィルムを貼ったメガネを使い、２眼式立体表示を行う方式をアナグリフという。この方式では同一画面上に赤色の光で構成される画像Aと、青色の光で構成される画像Bとを重ねて表示する。すると、赤色のフィルムを通すと赤で描かれたものは見えなくなり、青色のフィルムを通すと青で描かれたものは見えなくなる。人間の脳は見える画像の違いを前後の広がりと解釈し、立体感があるように見える。

この問題では、赤色のフィルムを通した右目には青色の光で構成される画像Bが見え、青色のフィルムを通した左目には赤色の光で構成される画像Aが見える。これによって鑑賞者の両目に視差のある画像が提示されるため、立体的な像をみることができる。

後半はこの原理を使って、映像が「浮かんで見える」か、「奥まって見える」かを問うている。浮かんで見えるか、奥まって見えるかは、脳が画像Aと画像Bの重なり合うと意識する位置がスクリーンの手前か、奥かで決まる。それは、三角形の相似の問題へと帰着する。

以下に浮かんで見えるロゴと、奥まって見えるロゴの図の例を示す。それぞれ比較する三角形とその相似比から、右目用に表示するロゴの左端の位置（Rmm）と左目用に表示するロゴの左端の位置（Lmm）を求めることができる。

浮かんで見えるロゴの場合：Rmm = 290mm, Lmm = 310mm

奥まって見えるロゴの場合：Rmm = 386mm, Lmm = 374mm,

ただし、問われているX座標はピクセル単位で答える必要があるため、算出されたRやLにそれぞれ2を掛ける。

後半のアニメーション問題は、「最初はゆっくり、次第に速くなり、その後再び減速していき、最終的には停止する」という条件がヒントとなっている。選択肢はすべてtを変数とした関数zであるから、tが0から１まで変化した時の、zの変化の仕方を考えればよい。微分（数学Ⅱ）で学んだ増減表などで確かめることもできるが、条件を満たすのはtの３次関数である（４）だけである。

情報-5

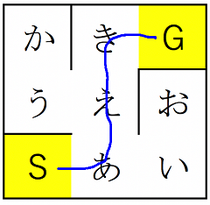
n×nのマス目を用いた迷路探索の問題である。問題文の（ア）には「分岐点に来た時、とりあえずどれかの方向を選んで先に進み、行き止まりになったら戻って別の方向を試すような」アルゴリズムと書かれている。これは“深さ優先”と言われる探索アルゴリズムである。例えば下図の迷路を考える。

スタート(S)からゴール(G)まで最短で次のようなルートが考えられる。

S → あ → え → き → G

一方で、選んだ方向が行き止まりだと効率が悪く、例えば次のようなルートになってしまう可能性もある。

S → あ → い → お → い → あ → え → う → か → う → え → き → G

この問題は次のような木構造を用いて考えることも可能である。

この問題を解くカギは、問題文の「あるマス目Pに対し、R（P）はPから移動できるマス目の集合である」の理解にある。集合の要素（移動できるマス目）は条件によって刻々と変化するのであるが、それがなぜゴールへ向かう道へと修正されるのかを理解することで、プログラムが作れるようになる。具体的には２つの条件が重要である。

条件1：辿って来たマス目はその集合から削除する

条件２：移動するマス目の候補がなくなったら（すなわち、空集合になったら）一つ戻る

上記の例では移動できるマス目の集合の初期状態が、

R(S) = {あ}

R(あ) = {S, え, い}

R(い) = {あ, お}

R(お) = {い}

R(え) = {あ, お, き}

・・・・

と定義されているが、

条件１によってSから辿って来たことでR(あ)={S, え, い} − {S} = {え, い}となって次のマス目は「え」か「い」となる。次に誤って「い」に進むと、行き止まりの「お」まで行くしかなくなるが、それぞれに、移動できるマス目はなくなりR(い) = R(お) =φ（空集合）となるので、条件2より「あ」まで戻る。するとR(あ)={え}となっているので、ゴールに繋がる道を進むことになる。

（ア）このことを、プログラムに置き換える。プログラムには変数としてXi, Yi, iが使われているが、Xiが「今いるマス目」、Yiが「移動できるマス目の集合」、カウンタ変数iが正しい道順の順番である。

（イ）処理Cは正しいルートを作るための処理であるから、その実行回数が最小ということは、最短経路を辿ったときの実行回数である。上記の例では「S → あ → え → き → G」のG以外のところで実行されるから、最小値は4回（3×2– 2）である。この式を大きさnとして一般化すると、n×2– 2＝2n–2回となる。

処理Bは道を誤って後戻りするための処理であり、その実行回数が最大ということは、正しいルートを除いたすべてのマス目で後戻りの処理を行ったことを意味する。大きさ3の迷路の場合、ゴールを除いた８マスから正しいルートの４マスを引いた、４が処理Bの実行回数の最大値である。大きさnの迷路場合、ゴール以外の全（n² – 1）マスから正しいルートで用いた（2n – 2）マスを引いた、n² – 2n + 1が処理Bの実行回数の最大値である。