慶應義塾大学総合政策学部・環境情報学部（以下、慶應義塾SFC）の入試は、(1)「数学または情報」と「小論文」、(2)「外国語」と「小論文」、(3)「数学および外国語」と「小論文」の3とおりの中から1つを選択します。「数学または情報」については、試験当日に試験教室でどちらかを選択します。つまり、慶應義塾SFCには、「情報」と「小論文」だけで入学することができるのです。

慶應義塾SFCは、本番の入試に向けて、2014年と2015年に「情報」の参考試験を実施しています。それらの概要については、情報処理学会・情報入試研究会・河合塾で共同制作した解説動画（※）を公開しているのでご参照ください。

※「情報」入試対策＜14・15年 参考問題解説＞

さて、慶應義塾SFCの2016年度入試は、2月17日に総合政策学部、翌18日に環境情報学部の試験が行われました。「情報」の受験者数は両学部あわせて二百数十名ほどいた模様で、1回目の情報入試としては満足できる数ではなかったかと推察されます。

では、情報入試問題がどのようなものであったか概観すると、両学部ともに大問4つ（I～IV）で構成されており、全問必答。第一印象は「簡単」であるが、問題に取り組み始めると「なかなか難しい」と感じ、最終的には「納得」できる、非常に良問だと総括できます。

Iは情報セキュリティや情報関係法規などの知識、IIは情報科学の基礎、IIIはデータベースやネットワークなどの応用、IVは日本語で処理手順を記述するいわゆるプログラミング能力をそれぞれ問うものでした。以下、個別に見ていきます。

◆慶應義塾大学入試問題

•2016年度 総合政策学部

•2016年度 環境情報学部

　※情報入試研究会のサイトより

総合政策学部

総－情報−I

説明を読んで用語を答えるものと、説明文の正誤を判断する問題で構成されている。前者は知識があるかないかで決まってしまう。後者は思索を巡らせれば正解の選択肢をかなり絞り込めるが、誤答選択肢がうまく設定されているので択一する際に迷った受験生も多かったのではないだろうか。ただ、非常に身近な題材だったので、その点は考えやすかっただろうし、知っておくべき知識でもある。

総－情報−II

通信速度、2進表現、並べ替えについて問うている。(イ)は、各カードが2進表現の各桁に対応していると気づけば易しい問題である。(ウ)の最後の問題は出題ミスとして処理されたが、比較の回数ではなく、交換の回数を問いたかったであろうと推測できる。

総－情報−III

データベースのテーブル設計の問題であるが、これは問題をきちんと読めば、自ずと正解に到達できる極めて易しい問題だった。

総－情報−IV

(ア)は、タイムチャートをかけばわかりやすく、比較的簡単な問題だったが、(イ)は骨のある問題だった。一瞬面食らうが、処理Aと処理Cが共通であり、落ち着いて考えれば正解を導き出せる。

環境情報学部

環－情報−I

総－情報−Iと同じ傾向だったが、Winny事件の判決文を読んで理解するという、なかなかおもしろい問題が含まれていた。

環－情報−II

論理演算、数値表現、符号化について出題された。(ア)の2問目は(C+D)をひとかたまりとして考えてベン図を描画すれば比較的簡単に解ける。(イ)は2進法の基礎であり、(ウ)は2進化符号の典型問題である。

環－情報−III

インターネットのしくみについての知識を問う問題である。全体的に平易な問題だと言え、環境情報学部を目指すならこの程度の知識は持っていて然るべきだろう。

環－情報−IV

これは数学と情報の複合的な問題と言えるかもしれない。(ア)については、漸化式でnを0からある程度の数まで変化させ、関数ｆがどのような値を返すかを観察すれば、自ずと正解にたどり着く。(イ)は、(ア)の答えがわからなかったとしても、漸化式をそのまま日本語で記述すればよく、総－情報−IVに比べてかなり簡単だった。(ウ)は理由を説明するために必要な文を選択するというやや変わった形式だったが、平易な問題だったといえる。

まとめ

総合政策学部の問題は若干社会的、環境情報学部の問題は若干科学的な色を感じました。具体的な設問においては、「社会と情報」と「情報の科学」のどちらを受講していても、大きな有利不利は生じないと思われます。いかにも慶應義塾SFCらしい、とてもよく考えられている問題だと感じました。

 (中野由章)

2016年度慶応義塾大学（総合政策学部・環境情報学部）情報　解答例

総合政策学部

総－情報－I 

（ア）(1): 3（水飲み場型攻撃）

（イ）(2): 1（ワンクリック詐欺）

（ウ）(3): 4（ランサムウェア）　ランサム(ransom)は身代金の意。

（エ）(4): 3（パブリシティ権）

（オ）(5): 3

(1) 誤り：死者に関する情報は「個人情報」には含まれない。

(2) 誤り：特定の個人を識別できる画像は「個人情報」に該当する。

(4) 誤り：「個人情報」であるかどうかは、公表されているかどうかには関係ない。

(5) 誤り：「個人情報取扱事業者」は個人情報データベースなどを事業の用に供している者であり、私的な目的で管理している場合は該当しない。

（カ）(6): 2

(2) 誤り：保護者が申し出た場合はフィルタリングを利用しないことができる。

（キ）(7): 2

(1) 誤り：被害者の権利が侵害されたことが明らかである等一定の要件を条件として請求できる。

(3) 誤り：他人の権利が侵害されていると信じるに足りる相当の理由があったとき等の要件が必要である。 

(4) 誤り：他人の権利が侵害されていたことを知っていた場合は損害賠償責任を負う。

(5) 誤り：この法律では刑事罰についての規定はされていない。

（ク）(8): 3

(3) 誤り：「実用新案権」についての説明である。

（ケ）(9): 5

(1) 誤り：ソフトウェアメーカー等が定めた使用許諾契約によっては著作権の侵害に該当する。

(2) 誤り：著作権者の許諾を得ていない場合、私的使用目的であっても著作権の侵害に該当する。

(3) 誤り：Webページのリンクに許諾は必要ない。

(4) 誤り：音楽CDの製作者は著作隣接権によって保護されている。

（コ）(10): 4

(1) 誤り：2014年に成立したいわゆる「リベンジポルノ防止法」で規制されている。

(2) 誤り：フィルタリングの有無によらず、誰もがインターネットで情報を発信できるため、伝える情報の信憑性や表現に配慮することが必要である。

(3) 誤り：SNS上での付きまとい行為等ネット上での行為に関しては規制対象となっていない。

(5) 誤り：他人のパスワードを許可なく第三者に教える行為はこの法律で禁止されている。

総－情報－II 

（ア）

(11): 3（Gbps）　 (12)(13)(14)(15)(16)(17)(18)(19): 1048576

MiBはメビバイト(mebibyte)の略で2²⁰=1048576バイトを表す。

（イ）

(20)(21): 06　 (22)(23): 41　 (24)(25): 06　 (26)(27): 15

n 枚のカードがあるとき、そのうち何枚かを選ぶ場合の数は、各々のカードについて選ぶか選ばないかの2通りがあることから、一枚も選ばない場合を除くと全部で 2ⁿ-1 通りである。n 枚のカードで1から63までの63種類を表すためには 2ⁿ-1≧63 つまり n は6以上である必要がある。

例示されている4枚のカードが、1から15までを2進法で表したときにA: 1の位、B: 2の位、C: 4の位、D: 8の位が1である数がそれぞれ記入されていることに着目すると、次のように6枚のカードで目的を達成できることがわかる：A, B, C, D, E, Fのカードにそれぞれ1, 2, 4, 8, 16, 32の位が1である数を記入する。

（例）(43)₁₀=(101011)₂なので、43はA, B, D, Fのカードに記入する。

よって、必要なカードがもっとも少ないのは6枚…(20)(21) のときである。またこのときA, B, C, D, E, Fのカードの最初の数はそれぞれ1, 2, 4, 8, 16, 32であるから一番大きいカードはFであり、Fには32の位が1の数 (100000)₂,…,(111111)₂ つまり (32)₁₀,…,(63)₁₀ が記入されているので、10番目の数は 32+(10-1)= 41…(22)(23) である。

カードに1回しか現れない数は、2進法で表した6桁以下の数のうち1がちょうど1回現れる数であるから、全部で6個…(24)(25) であり、2回現れる数は1がちょうど2回現れる数であるから、全部で₆C₂ = 15個…(26)(27) である。

（ウ）

(28): 4 　(29): 2　 (30): 2　 (31)(32): 06　 (33)(34): 04　 (35)(36): 00　 (37)(38): 10

5個のデータのうち隣り合った2個のデータは4組…(28)（=5-1）あるので、これが一度ずつ調べた場合（以下、「1周比較した」などという）に比較する回数である。1周目の比較では、文中の通り41と12、77と11の2回…(29) 交換が行われている。1周目の比較後のデータは31, 12, 41, 11, 77であり、これに2周目の比較を行うと31と12、41と11の2回…(30) 交換が行われ、比較後のデータは12, 31, 11, 41, 77である。3周目の比較では31と11のみが交換され12, 11, 31, 41, 77に、4周目の比較では12と11のみが交換され11, 12, 31, 41, 77になる。これは順番どおりなので、5周目の比較では交換は行われず、操作が終了する。交換は全部で2+2+1+1= 6回…(31)(32)　行われている。

5個の数字が最初から順番どおりに並んでいる場合は、1周比較するのみで比較は4回…(33)(34) であり、交換は0回…(35)(36) である。逆の順番で並んでいる場合は、5個のデータから2個選んだ組合せそれぞれについて1回ずつ交換が行われることになるので、交換は全部で₅C₂ = 10回…(37)(38) 行われる(注)。

※注：交換の操作を直接数えてもよい。実際に操作を行うと、5周比較が行われ、交換はそれぞれ4, 3, 2, 1, 0回行われることから、交換は全部で10回となる。

総－情報－III 

（ア）

(40): 4 （ポイント残高）　 (41): 6 （プレミアム会員登録日） （順不同）

問題文中に「ポイント情報、プレミアム会員かどうかなどの情報を管理するため」とあること、プレミアム会員は登録から100日間有効であるためプレミアム会員かどうかの判定に登録日が必要になることから判断できる。その他の項目は管理上必須の情報ではない。

（イ）

(42): 2 （単価）　 (43): 3 （販売開始日）　 (44): 4 （販売終了日） （順不同）

「過去にどの商品をいくらで販売したかを振り返る」目的であることから判断できる。

（ウ）

(45): 4 （使用ポイント数）　 (46): 6 （顧客ID）　 (47): 7 （商品管理ID） （順不同）

「どの会員がどの商品をどのような時期に購入しているのかを解析する」目的であることから、顧客情報と商品情報が必要である。顧客情報は「顧客管理テーブル」で管理していることから、顧客名ではなく顧客IDがより適当である。商品情報は「価格管理テーブル」で管理していることから、商品名ではなく商品管理IDがより適当である。また、「購入・ポイント利用履歴テーブル」という名称と、使用ポイントは購入ごとに管理が必要であることから、残りの1項目は使用ポイント数が適当であると判断できる。

（エ）

(48): 1 （顧客管理テーブル）

顧客管理テーブルにある「プレミアム会員」及び「プレミアム会員登録日」は、新規プレミアム会員登録やプレミアム会員登録から100日経過することで書き換えられる。

（オ）

(49)(50): 18 （総購入額）

(51)(52): 24 （ポイント残高） （(49)(50), (51)(52)は順不同）

(53)(54): 21 （商品管理ID）

(55)(56): 15 （購入・ポイント利用履歴テーブル）

(57)(58): 14 （使用ポイント数）

(59)(60): 16 （顧客管理テーブル）

(61)(62): 24 （ポイント残高）

使用ポイントは総購入額に対して決めているが、「購入・ポイント利用履歴テーブル」への記録は商品ごとに行う必要があるため、購入商品ごとにその商品の購入額を超えないように使用ポイントを割り振っている。

図：（例）500ポイント使用

総－情報－IV 

（ア）

(63)(64)(65): 066　 (66): 3 （C）　 (67): 5 （E）　 (68): 1 （A） （(66), (67)は順不同）

各作業が終わるまでの最短時間は次のように計算できる：まず先行作業が無い作業は所要時間が最短時間である。先行作業がある作業Xは、先行作業の最短時間のうち一番長いものにXの所要時間を足したものが最短時間である。例えば、作業Dの最短時間は、先行作業A, Bの最短時間のうち長い方の30分にDの所要時間30分を足した60分である。最短時間は次の表のように整理でき、T_min はHの最短時間である66分…(63)(64)(65) である。 

Hの先行作業のうち最短時間が長いG、Gの先行作業のうち最短時間が長いD、Dの先行作業のうち最短時間が長いBは所要時間が1分でも延びるとT_min も長くなる。Fの所要時間が5分延びると最短時間が 63+5=68 分となり T_min も長くなる。残りのA, C, Eについて次の表の通り調べると、所要時間が5分延びても T_min が変わらないが10分延びると変わるのはC…(66)とE…(67), 所要時間が10分延びても T_min が変わらないが15分延びると変わるのはA…(68) であることがわかる。

（イ）

(69)(70): 28 （すべての作業の集合）　

(71)(72): 27 （空集合）　

(73)(74): 14 （P(x)）

(75)(76): 19 （M(y)）

(77)(78): 16 （M(x)）

(79)(80): 15 （T(x)）

(81)(82): 11 （x）

(83)(84): 22 （M(z)）

(85)(86): 23 （T_min=T_delay）

(87)(88): 29 （1増やす）

(89)(90): 29 （1増やす）

(91)(92): 13 （D）

処理Aは各作業 x について、（ア）で述べた最短時間 M(x) を計算している。集合 U はまだ最短時間が計算されていない作業の集合であり、処理Aを行うたびに属する作業が減っていく。処理Bは作業 w の遅れ D を1分ずつ増やしていって、完成時間 T_delay がもともとの完成時間 T_min より大きくなるかどうかを判定しており、初めてT_min=T_delay でなくなったときの遅れ D が求める出力となる。

■環境情報学部

 環－情報－I 

（ア）(1): 3（パスワードリスト攻撃）

（イ）(2): 1（ゼロデイ攻撃）

（ウ）(3): 5（サイバーセキュリティ）

（エ）(4): 5

(5) 誤り：携帯電話としての契約が終了したスマートフォンであっても、Wi-Fi等のインターネット接続サービスは使用可能であるから、セキュリティ上の問題が発生しうる。

（オ）(5): 1

(2) 誤り：「特定電子メール法」によって規制されている。

(3) 誤り：返信することで個人情報が業者間で流通する可能性があるため、返信してはいけない。

(4) 誤り：「特定電子メール法」によってオプト・イン方式が認められている。

(5) 誤り：プロバイダ等による迷惑メールをブロックするサービスは認められている。

（カ）(6): 4

(1) 誤り：「プロバイダ責任制限法」でプロバイダの損害賠償責任を免責する規定がある。

(2) 誤り：一定の要件の下で発信者の情報開示を行うことができる。

(3) 誤り：SNS上で発信者の個人情報が特定される事案も問題となっている。

(5) 誤り：「プロバイダ責任制限法」等の法規制が整備されている。

（キ）(7): 3

(1) 誤り：芸術性の高い建築物は著作物として著作権で保護される対象となる。

(2) 誤り：事実の伝達にすぎない時事の報道は著作物に該当しない。

(4) 誤り：表現されたものであれば著作物に該当する。

(5) 誤り：素材の選択又は配列によって創作性を有する編集物は著作物に該当する。

（ク）(8): 3

(3) 誤り：写真に写っている友人にも肖像権はあるため、無断投稿は肖像権の侵害に当たる。

（ケ）(9): 2

(2) 誤り：個人情報の流出事案が発生した場合、個人情報を適正に管理していなかったとして企業が賠償責任を負う可能性がある。

（コ）(10): 3

(1) 誤り：ソフトの提供行為について幇助犯が成立する可能性があると説明されている。

(2) 誤り：説明されているのは公開、提供行為についてであり、開発行為は触れられていない。

(4) 誤り：「ソフトを入手する者のうち例外的とはいえない範囲の者が…著作権侵害に利用する蓋然性が高いと認められる場合」という説明から、関係があると考えられる。

(5) 誤り：「実際にそれを用いて著作権侵害（正犯行為）が行われたときに限り」という説明から、関係があると考えられる。

 環－情報－II 

（ア）

(11): 1（A） (12): 3（B） （(11), (12)は順不同）

(13): 4（B） (14): 5（C） (15): 7（D） （(13), (14), (15)は順不同）

となる。なお、最後の等式は一般に

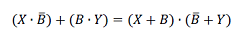
となることからわかる。

（イ）

(16)(17)(18): 127

(19)(20)(21): -29

(22)(23)(24)(25)(26)(27)(28): 1110100

(29)(30): 14（d）

(31)(32): 17（aとd）

0と正の整数のみを表現する場合、7ビットの2進数の最大値は (1111111)₂= 127…(16)(17)(18) である。

補数表現を用いる場合、1100011 は最初の1ビットが1であるから負の数を表しており、その絶対値は 100011 を反転させた (011100)₂=28 に1を加えた 29、よって表す数は、−29…(19)(20)(21) である。

同様に、−12を補数表現を用いて7ビットの2進数で表すには、11を2進数で表した001011を反転させた110100に負の数を表す1を付加して、1110100…(22)(23)(24)(25)(26)(27)(28) とすればよい。

0と正の整数のみを表現した2進数の場合、末尾の2ビットが4で割った余りを表すので、4の倍数は末尾が00の(d)…(29)(30) のみであるとわかる。

2進数の小数表示において誤差を生じないことは、既約分数で表した場合に分母が2の累乗（1, 2, 4, 8, ...）になることと同値である。選択肢の10進数を分数で表すとそれぞれ 進数を分数で表すとそれぞれ

(a): 1/10　 (b): 1/4　 (c): 33/8　 (d):  321/40 

であるから、このうち分母が累乗でないものは(a)と(d)…(31)(32) である。

（ウ）

(33): 4（D）　 (34): 1（A）　 (35): 4（D）　 (36): 4（D）　 (37): 3（C)

(38)(39): 23（aとcとd）　 (40).(41)(42): 1.90

{ 00, 01, 1, 0 }という変換において、00011の末尾の1は必ずCになることに着目すると、元の文字列の可能性は00|01|1：ABC, 00|0|1|1：ADCC, 0|00|1|1：DACC…(33)(34), 0|0|0|1|1：DDDCC…(35)(36)(37) のいずれかであることがわかる。

(a)～(d)の変換方式について、

(a): 全ての文字が3ビットに変換されていることから、3ビットずつ区切れば復元できる。

(b): 110がDAとCの2通りに復元されることから、一意ではない。

(c): 変換後の2進数の末尾3桁に着目すると、010なら末尾はA、 110ならもう1ビット見て0110ならDで1110ならA、011ならB、111ならC、000, 100, 001, 101にはなり得ないので、末尾の文字が一意に復元できる。これを繰り返せば元の文字列が一意に復元できる。

(d): 各文字を変換すると末尾が1であるから、変換後の2進数を上の桁から見ていって1が出てきたところで区切れば一意に復元できる。

よって、一意に復元できる変換方式はaとcとd…(38)(39) である。

A, B, C, Dの出現割合が4:3:2:1のとき、全体に占める各文字の割合は0.4, 0.3, 0.2, 0.1であるから、{ 1, 01, 000, 001 }という変換方式を用いた場合に期待される1文字あたりのビット数は

0.4×1+0.3×2+0.2×3+0.1×3= 1.90…(40).(41)(42) である。

 環－情報－III 

(43): 2（ウェブブラウザ）　 (44): 4（URL）　 (45): 6（ドメイン名）　 (46): 8（DNS）

(47): 5（jp）　 (48): 6（TLD）　 (49): 2（ccc.keio.ac.jp）　 (50)(51)(52): 032

(53): 7（約43億） 　(54): 3（256）　 (55): 5（ネットワーク部）

(56): 2（ホスト部）　 (57): 7（最上位）

 環－情報－IV 

（ア）

(58): 1（ n を2進数で表した時の1の個数を値とする。）

小さい n に対して f(n) を計算すると n を2進数で表した時の1の個数であると予想できる： 

漸化式より、n が奇数のとき、n の2進数表示の末尾の桁を除いた数 (n-1)/2 より f の値が 1 増加し、n が偶数のとき、n の2進数表示の末尾の桁を除いた数 n/2 と f の値が変わらないことから、f(n) が n を2進数で表した時の 1 の個数であることがわかる。

（イ）

(59)(60): 11（0）

(61)(62): 18（ n=0 ）

(63)(64): 22（ n が奇数）

(65)(66): 20（ (n-1)/2 ）

(67)(68): 14（ a の値を1増やす）

(69)(70): 21（ n/2 ）

(71)(72): 13（ a ）

変数 a は 1 の個数をカウントするために用いている。処理Aでは n を偶奇で場合分けし、奇数の場合のみ a を 1 増やすことで 1 の個数をカウントしている。10進数を 2 で割ることを繰り返して2進数に直す手順と同様のアルゴリズムになっている。

（ウ）

(73): 2（ n₁ の値は0以上の整数である。）

(74): 4（ n_k が 0 以上の整数なら、n_k+1 も 0 以上の整数である。）

(75): 6（ n_k > 0 ならば n_k > n_k+1 が成り立つ。）

(76): 9（0 以上の整数からなる数列で、必ず前の項より次の項の方が小さい場合、無限に続けることはできない。）

選択肢(9)を用いることは容易に想像でき、n_k+1 は n の2進数表示から末尾 k 桁を除いた数であることから、{ n_k } が選択肢(9)の条件に合致する数列であることがわかる。